Welcome to Aquarius, Volume 8 (August 16, 2007), Squaring the Circle Exactly.

Quick Look Table of Contents for Constructions: (62 pages)

Values and constructions required for squaring the circle

The construction procedures required

Conversion from line length to ratio

Conversion from ratio to line length

Square of a value

Square root of a value

Square root of a product of two values

[Squaring-the-circle exactly] construction steps

VALCON PAGE LINK 1: [Squaring-the-circle exactly]

Begin the constructions with the five-sixths constructions: Constructions #1, #2, and #3.

The nine-elevenths construction: Construction #4

The point fifty-five (0.55) constructions: Constructions #5 and #6

The (secant 18)^4 constructions: Constructions #7 and #8.

[My specific claim of discovery] and the key to the theory and the solution.

Then Construction #9.

VALCON PAGE LINK 2: [My specific claim of discovery]

The Key to the Theory and Solution Between Constructions #9-2 and #9-3

Construction of 0.7778, as well as 7.778 and 0.2222, 2.222, and 1.222 and 8.778.

Construction #10, a set of constructions.

[The Definition of M and MQ] (MQ = M^2)

VALCON PAGE LINK 3: [The Definition of M and MQ]

[The Construction of TN and NT] Construction #11

[The Construction of MQ and M] Constructions #12 through #16

VALCON PAGE LINK 4: [The Construction of MQ and M]

[The Get Pi constructions] Constructions #17 through #20

VALCON PAGE LINK 5: [The Get Pi constructions]

[The Exactly Pi and 1] constructions (improved from Volume 1 of Welcome to Aquarius)

VALCON PAGE LINK 6: [The Exactly Pi and 1]constructions

The Pi and MQ Constructions (alternative square = circle area)

A New Definition of Pi

MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM

Values and Constructions required for squaring the circle:

Notation and construction of similar triangles (re-construction of a right triangle):

S=sine CS=cosecant C=cosine SC=secant T=tangent CT=cotangent

The reality of re-constructing right triangle angles and sides:

Construct A, and: A=A -------------->B=A*cotangent----->H=A*cosecant

Construct B, and: A=B*tangent----->B=B ----------------->H=B*secant

Construct H, and: A=H*sine -------->B=H*cosine--------->H=H

(Below, G = angle of interest, OPP = opposite angle in a right triangle.)

sin = A/H = 1/csc, csc=H/A = 1/sin, sin G = cos OPP, csc G = sec OPP

cos= B/H = 1/sec, sec=H/B = 1/cos, cos G = sin OPP, sec G = csc OPP

tan= A/B = 1/cot, cot=B/A = 1/tan, tan G = cot OPP, cot G = tan OPP

X * sin = X/csc,----->X * csc = X/sin

X * cos = X/sec,---->X * sec = X/cos

X * tan = X/cot,----->X * cot = X/tan

(ratios can be converted to line lengths and line lengths can be converted to ratios):

Cosine 36 = 0.809016994374947424102293417182819... times 2 = Phi

Phi = 1.61803398874989484820458683436564... and inverse is

phi = 0.618033988749894848204586834365638... or "little phi" or 1/Phi

and = (Sine 18) * 2, Sine 18 = 0.309016994374947424102293417182819...

also, (Sine 18) = (Cosine 36) minus 0.5

(phi)^2 = 0.381966011250105151795413165634362...

phi + (phi)^2 = 1 (known to all mathematicians and geometers)

(Phi)^2 = 2.61803398874989484820458683436564... = (1.618033988...)^2

and (Phi)^2 / 2 = (sine 18) + 1 = 1.30901699437494742410229341718282...

and note that (sine 18) + 0.5 = 0.809016994374947424102293417182819...

Also, Phi is the limit of the Fibonacci series: 1+1, 2+1, 3+2, 5+3, 8+5, 13+8, and so on, where the last sum divided by the previous sum = 1.618033988... as the sums grow larger. Previous sum divided by last is inverse (0.618033988...).

Begin with phi = 0.618033988749894848204586834365638...

(Pi*Ho) = 3.14460551102969314427823434337184... = 4 times sqrt(phi)

sqd = 9.88854381999831757127338934985021... = 16 * phi

(Pi*Ho)/ 4 = sqrt(phi) = 0.786151377757423286069558585842959...

FX = (5/6)=0.833333333333333333333333333333333...

sqrt(5/6)=0.912870929175276855761616304668004...

SX = (6/5)=1.2

sqrt(6/5)=1.0954451150103322269139395656016...

Phi^2=2.61803398874989484820458683436564... (also = Phi +1)

divided by Pi =0.833346100984274536545032628319445...

which = (5/6) * MQ, where MQ = 1.00001532118112944385403915398333...

and sqrt(MQ) = M= 1.00000766056122262280424348031297...

or M = 1.000007661...

QM = inverse of MQ = 0.999984679053605550929814794430672...

which = Pi * VP, or Pi * 0.318305009375087626496177638028635...

and VP = (5/6) * (phi)^2 or (5/6) * 0.381966011250105151795413165634362...,

therefore VP = 0.318305009375087626496177638028635...

and (phi)^2 = (0.618033988749894848204586834365638...)^2

= 1/ 2.61803398874989484820458683436564... = (phi)^2 because I use upper case and

lower case to distinguish phi [0.618033988...] from Phi [1.618033988...]

Note that a hand-held scientific calculator may show Phi as 1.618033989...

Variations in the decimal value of MQ (after the ninth digit):

Later, we will see that our construction of MQ will yield a slightly different value that has

different decimal digits following the 9th decimal digit, due to the limitations of the precision of the math processor in a desktop computer. My desktop computer writes the constructed line MQ as 1.00001532123408073944164930824006... . The first version of MQ, above: 1.00001532118112944385403915398333..., is the result of using the computer calculator to obtain Phi^2, and then dividing by Pi, and by (5/6). The difference in decimal digits following the ninth decimal digit is due to the limited precision of the calculator. Limited, but still good to the ninth place (billionths).

PF=0.55 (label for this value derived from "Point Five")

ES= (1/0.55)=1.81818181818181818181818181818182...

(label for this value derived from "Eighteen Series")

*1.2 = 2.18181818181818181818181818181818...

*1.2 = 2.61818181818181818181818181818181...

*1.2 = 3.14181818181818181818181818181818...

*1.2 = 3.77018181818181818181818181818181...

*1.2 = 4.52421818181818181818181818181818...

*1.2 = 5.42906181818181818181818181818181...

*1.2 = 6.51487418181818181818181818181818...

And, 2.618181818... = 432/165, and 3.618181818... = 864/275

LN= (11/9) = 1.22222222222222222222222222222222... (eLeven Nines)

NL = 0.818181818181818181818181818181818... (Nine eLevenths)

* 1.2 = 0.981818181818181818181818181818182...

SF = (secant 18)^4 = 1.22229123600033648574532213002996...

(label for this value derived from Secant 18 to Fourth power)

inverse of SF = FS = 0.818135621484342140063933385739262...

sqrt of that = (cosine 18)^2 = 0.90450849718747371205114670859141...

and that = (Phi/4) + 0.5 [0.5 + 0.40450849718747371205114670859141...]

TN= SF/LN = 1.00005646581845712470071810638815...

NT, inverse of TN = 0.999943537369751504522585249236876...

(labels "TN" and "NT" from mind of author)

The value 0.2222 (stopped there at 4th decimal place)

The value 0.7778, = 1 - 0.2222 --->(when printed, p. 5)

Also, 1.222 and 8.778 and 0.1222 and 0.8778

These values, from LN to 0.7778, in particular TN and NT, possess unique properties that reveal the meaning of proportion.

The construction procedures required include dividing a line in half, doubling a line or increasing line length by adding a length. Also, re-construction of right triangles, meaning construction of similar right triangles with the same angles and trigonometric ratios but with different, proportional, side lengths, and the squaring-of-the-rectangle construction. It is therefore both surprising and simply elegant that no new or unique construction is required to square the circle. This is true because we square the circle through the discovery of the identity of M (1.000007661...) and the re-discovery of proportion. The method for dividing a line in half is commonly known. Descriptions of how to construct a similar right triangle, and how to "square the rectangle," given in Volume 1, are repeated here for your convenience.

Important note on construction steps:

Since these well-known procedures are all that is needed, they will not be described repeatedly in detail for each time they are used, but will simply be stated as "re-construct the [designated] right triangle," or construct a rectangle with specified width (height) and length (horizontal side), and then "square the rectangle." Detailed construction examples with drawings are given in Volume 1, Precision of the Ancients. Drawings are also provided here in Volume 8 with the actual "squaring-the-circle exactly" construction steps.

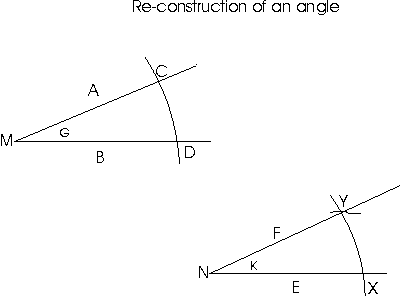
Reconstruction of an angle (for construction of similar right triangles):

Given angle G, lines A and B meeting at vertex M, construct straight line E where needed. Locate new vertex N on E. On given angle, open compass to useful radius (R), with pivot on vertex M, draw the arc across both sides of the given angle (points C and D). With the compass pivot at point N on line E, draw that same arc across and above line E (creating point X on line E). With the compass pivot on point C on the given angle, open the compass scribe to point D on the given angle. With this new radius of distance between C and D, place the compass pivot on point X on line E and draw the new arc to intersect the other arc that was previously drawn with the pivot on point N. Designate that point of the intersection of the arcs as point Y. Then, construct the straight line from vertex point N to point Y, that line being line F, and therefore line E and F meeting at vertex N create the same angle as the original angle G. Angle K = angle G.

We construct a similar right triangle by re-constructing the angle of interest or the angle opposite the angle of interest and then the right angle, or we may construct the right angle first, and then the other angle, usually called an "acute" angle (less than 90 degrees).

Conversion from line length to ratio:

There are several ways to convert the value of a line length to a ratio by using the SRT Construction Table above. This is one example. Construct the starting line length (SL) such as 2.3, or 1.414213562... or 1.732050808..., as side A1 (Altitude) of a right triangle and side B1 (Base) as line length of 1. The tangent of that right triangle is then equal to the length of side A1. The inverse ratio of 1/A1 is therefore the cotangent. Having constructed this ratio, we can now multiply this ratio by another value (X) by constructing a similar right triangle with side B2 having a line length of X. Side A2 in our similar right triangle will then have a length equal to X*tangent, and the tangent equals our original side A1. Therefore, X*tangent = A2 = X*A1. (No drawing here.)

Conversion from ratio to line length:

There are several ways to convert the value of a ratio to a line length by using the SRT Construction Table above. This is one example. Starting with a ratio of 1.37, with A1 (Altitude) equal to 2.74 and side B1 (Base) equal to 3.7538, we have a cotangent ratio (B1/A1) of 1.37. We want to construct a line length of 1.37. We construct perpendiculars with one line approximately horizontal. On the side representing the Altitude (A2) of our similar right triangle, we mark off a length of 1. At the upper end point of A2 we then reconstruct the angle opposite side B1, which is the angle that has a tangent of (1/cotangent) or (1/1.37) or 0.729927007... . The other side of our reconstructed angle opposite A2 is then the Hypotenuse H2 of our similar right triangle, and our new Base side B2 must have a length of 1.37 because the cotangent = (B2/A2) = 1.37 and we have given side A2 a length of 1.

Square of a value:

There are several ways to construct the square of a line length value using the SRT Construction Table above. This is one example. Construct a right triangle with side A1 = SV (Starting Value) and side B1 = 1. The tangent is SV. Re-construct the angle of interest (opposite side A1) for a similar right triangle, so that the tangent is the same but side B2 in the similar right triangle is marked off as equal to SV (side A1). Then construct the perpendicular for side A2 at the end point of B2. The tangent (A2/B2) of the similar right triangle is SV, but side B2 = SV and therefore the length of line A2 must be equal to SV squared.

Square root of a value:

The best procedure for constructing the square root of a line length is called "squaring the rectangle." It has been known for centuries. For the starting value SV, construct SV as the side of a rectangle with the other side having a line length of 1. Follow the procedure for squaring that rectangle and the side of the square resulting is of course the square root of SV. We can also use the line length of 2 as the other side of the rectangle and then the side of the resulting square will be sqrt(SV) * sqrt(2). We can use our SRT Construction Table and the ratio of sqrt(0.5) to multiply that side [sqrt(SV)*sqrt(2)] * [sqrt(0.5)] and we would then have a new line length of sqrt(SV).

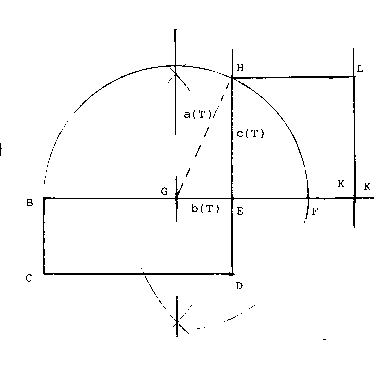
Remember that all rectangles and squares are parallelograms. Figure BCDE is a rectangle that I have constructed to represent BE and CD as a length of 2.5, and BC and DE as a width of 1. That makes the area of the rectangle 2.5. To construct a square of the same area, our first step is to extend the perpendiculars at E, line DE upward, and line BE to the right a distance greater than the width of the rectangle. Use the compass and place the pivot at intersection E and open the compass to the width of the rectangle. Then mark the same distance (width of the rectangle) on the line EF extended to the right. Now we treat the new line BF as though it were the diameter of a circle, and we bisect it to obtain the center G, so that BG = GF the radius of the circle. Use the compass to construct the upper half circle centered at G. It is not necessary to construct the lower half of that circle. The point H at which the extended DE vertical perpendicular intersects the circumference of the half circle is the length of the side of the square with an area of 2.5. Using the compass and straightedge, construct side HL parallel to EK and side LK parallel to EH. A measurement of the sides of the square, depending on the precision of construction, would show that the length of the side is the square root of 2.5 or 1.58113883... . There is also a statement (proof) that shows that for the sides of the right triangle a(T), b(T), c(T), c^2 = a^2 - b^2 , and the area of the rectangle equals BE * ED and that equals BE * EF, and line BE = (a+b) and line EF = (a-b), and therefore because c^2 = a^2 - b^2, c^2 also equals BE * EF the area of the rectangle. This is all beautifully described on pages 13 and 14 of Journey Through Genius, by William Dunham. It is also described in many other books about geometry, trigonometry and mechanical drawing or drafting.

What is rarely described in any book is that one can reverse this process and "rectangle a square," which can be very handy. The process of "rectangling the square" is based on the reality that if you construct a square to the right of the page, and extend the bottom side to the left (to point B in our drawing here). You can then mark off on that line the length of the rectangle you want (BE). You then construct a straight line from H to B, and then construct a perpendicular (right angle) at H and extend the perpendicular downward to intersect line EK at F. The line EF now equals the side (width) of the rectangle that will give us the area equivalent to the square. The procedure for "rectangling the square" serves as an alternate proof that this procedure is valid.

Square root of a product of two values:

This procedure is similar to the procedure for the square root of a given value SV, but in this case our starting value is the product of two values. For example, if we have a line length of 5.5, and we want to construct a line length that is the square root of (3.3 * 5.5), (18.15), we begin by constructing a rectangle with width of 3.3 and length of 5.5.

--> TOC [Back to VALCON TOC]

It is essential to keep in mind, all through these steps, that we do not need to invent any new construction procedure. All of the construction procedures are already established. The success in squaring-the-circle is achieved through seeing the numerical values, their proportions, and how to perform each calculation by construction. The constructions themselves will be familiar to geometers, and they will not be subject to "verification" by anyone. There is nothing new here in terms of construction procedures but they are written out in detail so that they are clearly identified as established procedures with the compass and straightedge. What you need to verify, is:

1) Are the calculations correct?

2) Can each calculation be performed precisely by a valid construction procedure?

Begin with the five-sixths constructions. The procedure of beginning with a tangent=2 right triangle with A1=2, B1=1, and H1=sqrt(5)and then re-constructing the tangent=2 right triangle with side H2=B1, A2=sqrt(0.8) and B2=sqrt(0.2)

yields the most useful set of line length values.

We have a line, the original H1=sqrt(5), that we can label as UN (uno) and designate as our line length of 1 for our construction purposes at this step. The second right triangle has B2=sqrt(0.2), which is 1/5 of UN, enabling us to readily construct line lengths of 0.8, 1.2, 1.8, and 2.2. Also, because B2 = (1/6) of (UN + B2) we can also construct ratios and line lengths of (9/11), (11/9), 1/(0.55) and 1/(0.45). We can also readily construct a ratio of (5/6) and then follow with construction of a line length of (5/6). Further, we have the ratio (and line length) of sqrt(0.2) and that value times (2 * [sine 36]) = (secant 18)/2. Therefore, it is also true that the ratio of our original pentagon side (length = 4* [sine 36]) to our original H1 (length = sqrt[5] ) is equal to (secant of 18), equal to 1.051462224... . The steps will all be described in detail for clarity.

Construction #1: (to get 1, 1/5, 1/6 and 5/6 values, together with Construction #2)

Construct perpendiculars, with base line approximately horizontal. Mark off length of B1 being approximately one inch for practical size of constructions, and A1 twice the length of B1. Construct the Hypotenuse line H1 from end point of B1 to end point of A1. Although approximately 2.5 centimeters (one inch) is the recommended practical length for our line B1 in Construction #1, WE DO NOT MEASURE ANY LINES. WE USE ONLY THE COMPASS AND STRAIGHTEDGE.

(G = angle of interest, OPP = opposite angle)

Facts for Right Triangle #1:

B1 = 1, A1 = 2, H1 = sqrt(5) = 2.236067978...

G = 63.43494882..., OPP = 26.565051177...

Sine = 0.894427191...sqrt(0.8)[4/5], Cosecant = 1.118033988...sqrt(1.25)[5/4]

Cosine = 0.447213595...sqrt(0.2)[1/5], Secant = 2.236067978...sqrt(5)

Tangent = 2.000000000, Cotangent = 0.500000000

Instead of constructing only the right triangle shown in the first drawing, continue the procedures for starting the construction of a pentagon. We will soon see that constructing the start of the pentagon now will be very useful for other required constructions.

Procedure for complete Construction #1: Construct perpendiculars as previously stated immediately above. Open the compass to a length of two times B1 to be the radius and construct the circle with its center at the intersection of the perpendiculars. On the horizontal line, mark off a length of B1 from the center point to the right, or divide the radius in half to the right of the center point. In the upper right quadrant of the circle, construct the straight hypotenuse H1 between the end points of A1 and B1. A1 is of course the radius (= 2*B1) and the upper half of the vertical perpendicular.

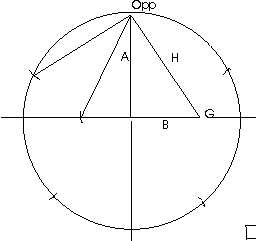
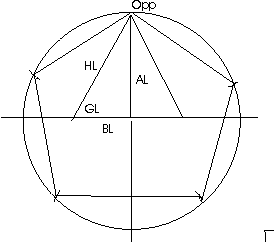
Next, to initiate the first step for construction of a pentagon, complete the "laying down the hypotenuse" procedure. Our right triangle in the upper right quadrant of the circle has a tangent of 2 with the vertex of the (tangent = 2) angle (63.434948822... degrees) to the right. With the pivot on that vertex point, open the compass the length of the hypotenuse (2.236067978... in proportion to B1), and swing the scribe from the upper vertex and upper end point of the hypotenuse, downward, and scribe a short curved line intersecting the horizontal perpendicular. I then designate the line to the left of the center point as Base BL of a right triangle to the left of our first right triangle, with the same Altitude, AL which is equal to A1. Construct the Hypotenuse HL of the right triangle in the upper left quadrant of the circle, the straight line between the upper end point of AL(A1) and the point just constructed by laying down the hypotenuse. Note that since B1 has a designated length of 1, and the full length of the line from the right vertex to the left vertex just constructed is 2.236067978..., then the length of the left Base BL must be that length minus 1, or 1.236067978..., which is the secant of 36 degrees. Therefore, the tangent of our left right triangle is 2/1.236067978..., which equals Phi (1.618033989...). The length of the Hypotenuse HL of the left right triangle is 2.351141009..., equal to 4 times the sine of 36 degrees.

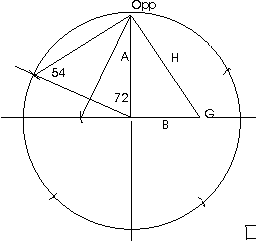
The next step in construction of the pentagon would be to place the compass pivot on the upper vertex of AL(A1), open the compass to the length of HL, and swing the scribe upward to the left and mark a short curve intersecting the circumference of the circle. The straight line from the upper vertex AL(A1) to that intersection point is then the side of the pentagon. This side is a chord that comprises one fifth of the circle, or 72 degrees. We do not need to construct the entire pentagon in order to make use of the isosceles triangle in the upper left quadrant which has two equal sides enclosing an angle of 72 degrees and the other two equal angles being 54 degrees. By dividing that 72-degree angle in half (described below) we create a pair of 36-54 degree right triangles.

NOTICE THAT THE RATIO OF THE SIDE HL (2.351141009..., ALSO THE SIDE OF THE PENTAGON) TO THE SIDE H1 (2.236067978...) IS THE SAME AS THE SECANT OF AN 18-DEGREE RIGHT TRIANGLE (1.051462224...). THIS WILL BE VERY USEFUL FOR CONSTRUCTION #8 COMING LATER.

Facts for the left right triangle in Construction #1:

BL = 1.236067978..., AL(A1) = 2, H1 = 2.351141009...

GL = 58.28252559..., OPP = 31.71747441... ( = 63.43494882... / 2)

Sine = 0.850650808..., Cosecant = 1.175570505... (2 * [sine 36])

Cosine = 0.525731112...(secant 18)/2, Secant = 1.902113033...([cosine 18]*2)

Tangent = 1.618033989..., (Phi) Cotangent = 0.618033989..., (phi)

Construction #2: (to get 1, 1/5, 1/6 and 5/6 values, together with Construction #1)

Re-construct angle G from the right triangle in Construction #1 with the angle vertex pointing to the right with the base line side being approximately horizontal. Mark off the line length of B1 on the Hypotenuse side H2, which is the upper side of the reconstructed angle. Construct a perpendicular to the base line from the upper end point of H2. This procedure is commonly known as "dropping a perpendicular" from a point above a line down to the horizontal line.

(Dropping a perpendicular.) With the compass open to a distance equal to H2 (equal to length of B1), and with the compass pivot on the upper end point of the Hypotenuse H2, swing the scribe to intersect with the base line at the vertex of G and at a second point on the base line to the left. With the compass pivot on one of these intersection points, and the compass open to a distance approximately equal to length H2, use the scribe to mark a curve approximately beneath the upper end point of H2 and below the base line. Place the compass pivot on the other intersection point and use the scribe to mark another curve that intersects with the previous curve marked below the base line. Then construct with the straightedge the perpendicular side A2 from the upper end point of H2 to the point of intersection of the curve marks below the base line. The perpendiculars and the point of intersection of the perpendiculars now give us Altitude A2 and Base B2.

Facts for Right Triangle #2:

B2 = sqrt(0.2) = 0.447213595..., A2 = sqrt(0.8) = 0.894427191..., H2 = 1 (B1).

G = 63.43494882..., OPP = 26.565051177...

Sine = 0.894427191...sqrt(0.8)[4/5], Cosecant = 1.118033988...sqrt(1.25)[5/4]

Cosine = 0.447213595...sqrt(0.2)[1/5], Secant = 2.236067978...sqrt(5)

Tangent = 2.000000000, Cotangent = 0.500000000

In Construction #2, the trigonometric ratios (or functions) are the same, of course, and the side lengths are different but exactly proportional. The precision of the particular compass and straightedge and the skill of the geometer are not the issue. If the constructions could be done perfectly, the results would be that perfect. This is the case with all geometric or proportional constructions.

Note the relationship between Construction #1 and Construction #2. Line length B2 is one-fifth (1/5) of line H1 (also labeled UN), and B2 is also one-sixth (1/6) of the line length of (UN + B2). Line length UN (our line H1) plus line length B2 = 2.683281573... IN PROPORTION TO OUR ORIGINAL BASE B1, IN CONSTRUCTION #1, BECAUSE B1 INITIALLY REPRESENTED A LINE LENGTH OF 1 IN PROPORTION TO H1, THE HYPOTENUSE H1 IN CONSTRUCTION #1, BECAUSE THE RATIO OF H1 TO B1 IS 2.236067978... [SQRT(5)] TO 1. And, sqrt(5) plus sqrt(0.2) equals (6 * B2). This may be obvious, but it needs to be emphasized, meaning that...

THIS IS AN IMPORTANT PART OF WHAT IS MEANT BY "PROPORTION IS EVERYTHING." THE RELATIONSHIPS THAT APPLY IN CONSTRUCTION #1 AND CONSTRUCTION #2 GIVE US THE FIRST RATIOS AND LINE LENGTHS THAT WE NEED TO BUILD OUR "INVENTORY" OF OTHER RATIOS AND LINE LENGTHS REQUIRED TO SQUARE THE CIRCLE.

Hereafter, the drawings of right triangles may include only the labels A, B, and H, and not designated triangle numbers, such as A3, B3, and H3. The numbers added to A, B, and H are used in the text to help associate the particular text with the numbered construction.

Construction #3 [to get (5/6) and (6/5) and other helpful values]

Continuing to designate UN as having a length of 1, and B2 as having a length of 1/5, we can now readily construct ratios and lines that will be essential for squaring the circle. We can readily construct the following lines/ratios:

(UN - B2) = 0.8 (4/5) >>>>>> ________ --->(when printed, p. 15)

UN = 1 >>>>>>>>>>>>>>>> _________

(UN + B2) =1.2 (6/5) >>>>>> ____________

(UN + UN - B2) = 1.8 (9/5) >> __________________

(UN + UN + B2) = 2.2 (11/5)> ______________________

Note, the lines drawn on the screen (or printed out) are not in exact scale to one another nor in proportion to the other drawings presented in these web pages.

We then construct a right triangle with Altitude A3 = UN and Base B3 = UN + B2. Construct the perpendiculars. With the compass, mark off the respective lengths of A3 and B3. We then construct a straight line from the end points of A3 and B3 to add Hypotenuse H3.

Construction #3 drawing:

Facts for Right Triangle #3:

A3 = 1 (UN), B3 = 1.2 (UN+B2), H3 = 1.562049935... [sqrt(2.44)]

G = 39.80557109..., OPP = 50.19442891...

Sine = 0.640184399..., Cosecant = 1.562049935...

Cosine = 0.768221279..., Secant = 1.301708279...

Tangent = (5/6), Cotangent = (6/5)

Note that the ratio of A3/B3 = the tangent = (5/6), and the cotangent is of course (6/5). We therefore can construct a line length of (5/6) as well as the line length of (6/5). Further, a line length of (UN + UN + B2) is equal to 11 times B2. And, line (UN + B2) divided in half equals (3 * B2). Therefore, the line length of (UN + B2 + [3*B2]) is equal to 9 times B2.

Dividing a line in half is one of the simplest of operations. Place the pivot of the compass on one end point of the line with the compass open to a distance that is about two-thirds of the line length. (The compass can be open, in fact, to any distance greater than one half of the line length). Rotating the pivot, let the scribe mark a curve that approximates a point above the half-length of the line and below the half-length of the line. Do the same with the pivot on the other end point so that the second pair of scribe marks intersect with the first pair. We then have two curved "X's," one above the half way point and one below. Use the straightedge to construct a straight line from the upper X to the lower X and that straight line is a perpendicular that intersects the original line at the point that divides the line into two equal halves. This procedure is the same as a commonly known method for construction of a perpendicular.

The nine-elevenths construction:

Construction #4: [ to get (9/11) and (11/9)]

For Construction #4, we will use the line (UN + B2 + [3*B2]) as Altitude A4, and the line (UN + UN + B2) as Base B4. Because (UN + B2 + [3*B2]) equals 9 times B2, and (UN + UN + B2) equals 11 times B2, the tangent of this right triangle is (9/11). The cotangent is of course (11/9).

Note the decimal values:

(9/11) = 0.818181818181818181818181818181818... (tangent)

(11/9) = 1.22222222222222222222222222222222... (cotangent)

Facts for Right Triangle #4:

A4 = (9*B2), B4 = (11*B2), H4 = (14.2126704... * B2)

G = 39.28940686..., OPP = 50.71059314...

Sine = 0.63323779..., Cosecant = 1.5791856...

Cosine = 0.773957299..., Secant = 1.292060946...

Tangent = 0.818181818..., Cotangent = 1.222222222...

The other trigonometric ratios for this right triangle may be of interest also, but not necessarily right now. Again, we have the ratios, therefore we can also construct line lengths of exactly the same values (0.818181818... and 1.222222222...).

The point fifty-five (0.55) constructions:

Note that we need line lengths and ratios of 0.55 and 0.45, because we want a line length of 1/0.55 and that equals 1.81818181818... and we can get that value by multiplying (9/11) by 2.22222222222... or by (1/0.45). Or, as follows in Constructions #5 and #6.

The value 0.55 = (2.2)/4 and 0.45 = (1.8)/4 and the lines/ratios of 2.2 and 1.8 have already been constructed through Constructions #1, #2, and #3.

Note that 0.55 =(2.2)/4 and therefore 1.818181818181... = 4/(2.2).

Also, 0.45 = 9/20 = ([9*B2]/[4*UN]), 0.55 = 11/20 = ([11*B2]/[4*UN]).

Construction #5: (to get 0.55 value)

For Construction #5, use the line length 2.2 for Altitude A5 and 4 (equals 4*UN) for Base B5. The tangent is 0.55. Construct perpendiculars. With the compass, mark off the lengths for A5 and B5 and then use the straightedge to construct the Hypotenuse H5 between the end points of A5 and B5. H5 = sqrt(20.84).

Tangent = (2.2/4) = 0.55

Cotangent = (4/2.2) = 1.818181818...

Facts for Right Triangle #5:

A5 = 2.2, B5 = 4, H5 = sqrt(20.84) = 4.564084884...

G = 28.81079374..., OPP = 61.18920626...

Sine = 0.481918749..., Cosecant = 2.075038584...

Cosine = 0.876215908..., Secant = 1.141271221...

Tangent = 0.55, Cotangent = 1.818181818...

Construction #6: (to get 0.45 value)

For Construction #6, use the line length 1.8 for Altitude A6 and 4 (equals 4*UN) for Base B6. The tangent is 0.45. Construct perpendiculars. With the compass, mark off the lengths for A6 and B6 and then use the straightedge to construct the Hypotenuse H6 between the end points of A6 and B6. H6 = sqrt(19.24).

Tangent = (1.8/4) = 0.45

Cotangent = (4/1.8) = 2.222222222...

Facts for Right Triangle #6:

A6 = 1.8, B6 = 4, H6 = sqrt(19.24) = 4.38634244...

G = 24.22774532..., OPP = 65.77225468...

Sine = 0.410364677..., Cosecant = 2.436856911...

Cosine = 0.911921505..., Secant = 1.09658561...

Tangent = 0.45, Cotangent = 2.222222222...

LET ME REMIND READERS AGAIN THAT THE DRAWINGS ON THE SCREEN AND PRINTED OUT ARE NOT TO SCALE AND NOT IN PROPORTION TO ONE ANOTHER. THE DRAWINGS ARE INTENDED TO GIVE A GENERAL IDEA OF HOW THE CONSTRUCTION WOULD APPEAR. IN ORDER TO SEE THE PRECISE PROPORTIONS THE READER WOULD HAVE TO COMPLETE ALL OF THE CONSTRUCTIONS AS DESCRIBED FROM BEGINNING TO END.

Please note that construction #5 and #6, the "point fifty-five" constructions, are not required specifically for squaring the circle, but the (1/0.55) line length (1.818181818...) enables the construction of the "sixth-fifths" or "Eighteen Series":

(1/0.55) = 1.81818181818181818181818181818182...

*1.2 = 2.18181818181818181818181818181818...

*1.2 = 2.61818181818181818181818181818181...

*1.2 = 3.14181818181818181818181818181818..., and so forth. This is a significant part of the reality of "proportion," which in theory is a field of knowledge separate from traditional mathematics or number theory.

The (secant 18)^4 constructions:

To get the value of (secant 18)^4, we begin with the construction that is the starting construction for the pentagon. Then we proceed to construction of the 36-54 degree right triangle, and then divide that to produce the 18-72 degree right triangle. Construction of the pentagon itself is not necessary for this step, but it is useful to look at the relationships of the pentagon and these right triangles.

Construction #7: (Construction of the 72-degree angle)--->(when printed, p. 20)

Procedure for Construction #7: Procedure is the same as for the complete Construction #1. Construct perpendiculars. Open the compass to any practical line length such as UN or (2*UN) for the circle radius and construct the circle. Steps that follow are same as for complete Construction #1. This Construction #7, or #1, provide the 72-degree angle.

Construction #8: (Construction of the 18-72 degree right triangle):

Steps for the 36-54 degree right triangle. We have already constructed a 72 degree angle in our complete Construction #1 and or #7. The drawing is shown here again.

Another view of the constructed pentagon:

A view of pentagon alone with upper right fifth divided in half:

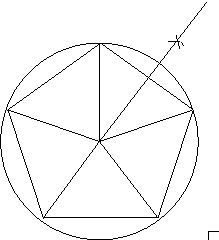
To divide the 72 degree angle in half we proceed as described below for dividing a 36 degree angle in half, which is the same procedure for dividing any acute angle in half.

A view of a separate 36-54 degree right triangle:

Divide the 36 degree angle in half: --->(when printed, p. 25)

The procedure for dividing an angle of 36 degrees in half is the same as for dividing any acute angle in half. Begin by reconstructing the 36-degree angle with the vertex V to the left. Open the compass to a practical distance and then place the compass pivot at the angle vertex V and then swing the scribe to intersect both arms, or sides, of the angle. Use the scribe to mark the intersection on the upper arm, at X, and then to mark the intersection on the lower arm, Y. At this point you could then construct a straight line from X to Y, but let that line be imaginary line Z. We then open the compass so that the distance between the pivot and scribe is about two-thirds of the distance from X to Y. Place the pivot on X and mark a short curve outward in the vicinity of the wider section of the angle so that the marked curve is approximately at the midpoint of the distance between the sides of the angle. Similarly, place the pivot on Y and mark a short curve that intersects with the first, and this intersection is point H (for Half). Use the straightedge to construct a straight line passing through that intersection H and the vertex V. Each angle created is now exactly one-half of the larger angle, and of course one-half of 36 degrees is 18 degrees. If line Z (between X and Y) were visibly constructed, H and Z would be perpendiculars.

We now have an angle of 18 degrees (one-twentieth of the circle) and can construct a right triangle with the following trigonometric ratios:

Facts for any 18-72 degree right triangle:

G = 18, OPP = 72

Sine = 0.309016994..., Cosecant = 3.236067978...

Cosine = 0.951056516...sqrt(0.2)[1/5], Secant = 1.051462224...sqrt(5)

Tangent = 0.324919696..., Cotangent = 3.077683537...

Note that the square root of 0.309016994... is 0.555892970..., which is one-half of the square root of 1.236067978..., or sqrt(secant 36)/2. And of course (secant 36) = sqrt(5) minus 1. The (cosecant 18) = 3.236067978... = sqrt(5) plus 1. The cosine, 0.951056516..., squared, = 0.904508497..., = 0.5 + (Phi/4).

It was good practice to divide the 36-degree angle in half so that we could construct an 18-degree right triangle. If we construct a right triangle with the acute angles being 18 degrees and 72 degrees, and the hypotenuse having a length of UN (1), then the altitude will have a length of 0.309016994... and the base will have a length of 0.951056516... . That value of 0.951056516... is of course the cosine and the secant is 1.051462224... . We want to use the secant value so that we can construct a line length of (secant 18)^4. However, we can use our construction for the start of the pentagon, in Construction #1, as a more convenient procedure for employing a ratio of 1.051462224..., but as the tangent of a right triangle.

--> TOC [Back to VALCON TOC]

(SPECIFIC ELEMENTS OF DISCOVERY I CLAIM)

The next step is Construction #9. Here at Construction #9 begin the eight constructions (#9 through #16) that I claim as my discovery of how to square the circle. Although constructions #1 through #8 are required to square the circle, they are not new and they are effective for squaring the circle only when used with constructions #9 through #16. I also claim as my discovery the definition of M and MQ, which I believe is the original purpose of the riddle, because M and MQ and the qualities of the secant of 18 degrees complete the unfolding and revelation of proportion. PLEASE NOTE THAT 18 DEGREES IS ONE FIFTH OF THE QUADRANT OF 90 DEGREES. The matter I claim is not found anywhere, in any language, prior to July 7, 2007.

I also claim that my work constitutes the re-discovery of proportion, but I do not ask any "experts" to confirm that. It may take many years to confirm or discredit this theory of "proportion" as a distinct science that is separate from the traditional number theory of mathematics.

Constructions #1 to #8 (Otherwise ordinary, known or "old" constructions.)

---------------------------------------dividing line---------------------------------------------------

Constructions #9 to #16 (New constructions, some used with old constructions, that involve performing calculations -- by construction -- that enable squaring the circle.)

Construction #9: [to get line length 1.222291236..., (secant 18)^4]

Instead of constructing the 18-degree right triangle, refer back to the complete Construction #1. If in that first construction we designate B1 as equal to 1, then A1 = 2 and H1 = sqrt(5). Apply the Pythagorean Theorem and you will see that the side of the pentagon has a length equal to 4 times the sine of 36 degrees. The side of the pentagon has a length of 2.351141009..., and we already know that H1 has a length of 2.236067978... . The ratio of 2.351141009... to 2.236067978... is 1.051462224..., the secant of 18 degrees. Therefore, we can construct a right triangle with an altitude equal to 2.351141009... and a base equal to 2.236067978..., and the tangent of that right triangle is of course 1.051462224..., the ratio we have use for.

Construct perpendiculars. With the perpendicular intersection to the left, take the two lines we need from Construction #1. First, open the compass to the length of the side of the pentagon (2.351141009...) and use the compass to mark that length as the length of Altitude A9 on the vertical perpendicular. Use the compass to get and mark the length of Base B9 as the original side H1 (2.236067978...). Construct the straight line between the end points of A9 and B9, the Hypotenuse H9. The angle G to the right is the acute angle of interest. The tangent of G is 1.051462224..., the same as the secant of 18 degrees. The length of H9 is sqrt(10.52786405...). Angle G = 46.4369994... degrees.

Facts for Right triangle #9:

A9 = 2.351141009..., B9 = 2.236067978..., H9 = 3.244667016...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

The next step is to re-construct this right triangle four times, so that we can obtain a line length, and ratio, equal to (1.051462224...) raised to the fourth power.

(Construction #9-1) [to get line/ratio = 1.051462224...]

Re-construct right triangle #9 but mark off the Base B9-1 with length UN (our designated line length of 1). The repetitive procedure here is: Construct perpendiculars. Mark off the new line length for Base B9-1 to the right of the intersection of the perpendiculars. At the right end point of Base B9-1, re-construct angle G. The upper side of the angle G, sufficiently extended, is the Hypotenuse of the similar right triangle. Altitude A always will be 1.051462224... times the length of Base B9-1.

Note that in similar right triangle #9-1, because the Base B9-1 equals UN, our Altitude A9-1 equals 1.051462224... in proportion to UN (ONE).

Facts for Right Triangle #9-1:

A9-1 = 1.051462224..., B9-1 = 1 (UN), H9 = 1.451059202...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

(Construction #9-2) [to get line/ratio = 1.105572809...]

Re-construct right triangle #9 but mark off the Base B9-2 with a line length equal to length A9-1 (1.051462224...) from Construction #9-1. Altitude A is 1.051462224... times the length of Base B or 1.051462224... squared, which equals 1.105572809... .

Facts for Right Triangle #9-2:

A9-2 = 1.105572809..., B9-2 = 1.051462224..., H9-2 = 1.525733937...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

(THE KEY TO THE THEORY AND THE SOLUTION.)

Why is the same drawing shown for these constructions 9-1 through 9-4? Because the differences in line lengths are very small, varying between approximately one-tenth and one-twentieth of the line length of one. This is evidence in support of my argument that the original purpose of the riddle (Can we square the circle?) was not only to square a circle, but was to lead us to an understanding of proportion. When we square the circle exactly, we are working with numbers of infinite precision. We cannot, in fact, square the circle exactly unless we are aware that there is such a value as Pi exactly. Or, we would have to believe that there is such a value as Pi exactly in order to square the circle exactly. The essence of the solution, presented here completely, does not establish how to write the number Pi exactly, but reveals that Phi squared is the product of Pi exactly, times (5/6) exactly, times MQ exactly. This is exactly what those who originally stated the riddle wanted us to learn. And it appears to me that struggling through the search for how to square the circle, to a successful conclusion, is the only way this reality can be discovered. This is why I persevered. As I said in the beginning, the stakes are high. Nothing less than the survival of our species, if proportion is in fact Nature's technology for producing all of the shapes that it produces, which leads naturally to how Nature produces all of the living tissues and living organisms it produces. In essence, if proportion is the sufficient cause of the self-organization of matter, then proportion is the sufficient cause of the evolution of life. This may appear to be an enormous "claim," but the subject matter is so immeasurably important it is wildly irresponsible to dismiss this claim by any means other than rigorous scientific study.

(Construction #9-3) [to get line/ratio = 1.162468045...]

Re-construct right triangle #9 but mark off the Base B9-3 with a line length equal to length A9-2 (1.105572809...) from Construction #9-2. Altitude A is 1.051462224... times the length of Base B or 1.051462224... to the third power, which equals 1.162468045... .

Facts for Right Triangle #9-3: --->(when printed, p. 30)

A9-3 = 1.162468045..., B9-3 = 1.105572809..., H9-3 = 1.604251598...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

(Construction #9-4) [to get line/ratio = 1.222291236...]

Re-construct right triangle #9 but mark off the Base B9-4 with a line length equal to length A9-3 (1.162468045...) from Construction #9-3. Altitude A is 1.051462224... times the length of Base B or 1.051462224... to the fourth power, or 1.222291236... . We have reached our target value in this line length of A9-4 [1.222291236...], for this construction.

A9-4 = 1.222291236... in proportion to UN.

Facts for Right Triangle #9-4:

A9-4 = 1.222291236..., B9-4 = 1.162468045..., H9-4 = 1.686809954...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

We are going to use 1.222291236... as a key value to construct a line length of MQ and then a line length of Pi and then square the circle. In terms of "seeing proportion," I wish to note here that this value [(secant 18)^4] when multiplied by (cosine 36) (by computation or construction) equals 0.988854382..., which equals (Pi*Ho)^2 / 10. These values of 0.988854382... and 9.88854382... can be the starting value for the next construction, which requires that we construct 7.778, and or 2.222, or 0.7778 and 0.2222, or 1.222 and 8.778, which values play a key role in constructing the value MQ. However, I am going to use a different starting value, the cosine of 36 degrees.

End of Construction #9.

Construction of 7.778, as well as 2.222, and 0.7778 and 0.2222, or 1.222 and 8.778

There are several ways to construct the line length that has the terminal digital value of 7.778, or 0.7778. I have chosen to begin with line length 0.809016994... (cosine 36). We will proceed toward the value of 7.778 by a process I call "sequential shaping."

Construction #10: (to get 0.7778 and 0.2222)

First, construct the 36-54 degree right triangle with the Hypotenuse H10 equal to our designated one value (UN). Re-construct the 36-degree angle with the vertex to the left, and mark off the length of UN on the upper side of the angle, to be the Hypotenuse H10. Drop the perpendicular from the upper end point of H10 down to the base line. The length of Base B10 is now 0.809016994374947424102293417182819... in proportion to our line length of UN (1).

Immediately following is a summary of the computations which we will perform next by construction using sequential shaping:

From --------> 0.809016994374947424102293417182819... --> - (2/5)

-0.4 = -------> 0.409016994374947424102293417182819... --> *5

*5 = ---------> 2.0450849718747371205114670859141... --> * 2

*2 = ---------> 4.09016994374947424102293417182819... --> -3.2 [16/5]

-3.2 = -------> 0.890169943749474241022934171828191... --> *5

*5 = ---------> 4.45084971874737120511467085914095... --> *2

*2 = ---------> 8.90169943749474241022934171828191... --> (-8.1) in two steps

-3.6 = --------> 5.30169943749474241022934171828191...

-4.5 = --------> 0.801699437494742410229341718281906... (-3.6, -4.5) = -8.1

then... -------> 0.801699437494742410229341718281906... --> +4

+4 = ---------> 4.80169943749474241022934171828191... --> /5

/5 = ----------> 0.960339887498948482045868343656381... --> /2

/2 = ----------> 0.480169943749474241022934171828191... --> +5, + 4 = +9

+9 = ---------> 9.48016994374947424102293417182819... --> /5, /2 = /10

/5 = ----------> 1.89603398874989484820458683436564... --> /2

/2 = ----------> 0.948016994374947424102293417182819... --> +4

+4 = ---------> 4.94801699437494742410229341718282... --> * 2

*2 = ---------> 9.89603398874989484820458683436564... --> - [sqrt(1.25) +1]

then ---------> sqrt(5)/2 = 1.11803398874989484820458683436564...,

+1 = ---------> 2.11803398874989484820458683436564...

then ---------> 9.89603398874989484820458683436564...

- 2.11803398874989484820458683436564...

= ------------> 7.778 (a "terminal digital value")

then, 7.778 / 5 = 1.5556, and 1.5556 / 2 = 0.7778, and 1 - 0.7778 = 0.2222

End of summary of computations to be constructed under Construction #10, which is a set of target-driven constructions rather than a single construction procedure.

Dividing by 10, or by 5, by construction:

First, the set of constructions for Construction #10 involve dividing a value by 10, or by 5 first and then by 2. There is more than one way to divide a value by 5, and I will use the method that we have already seen in action in the relationship between Construction #1 and Construction #2. That is, first construct the tangent=2 right triangle (the start of the pentagon construction) with the "dividend" value (value to be divided by 5) as the hypotenuse. You should see by now, if not understood previously, that with this right triangle, the proportional values of the sides are A1 = 2, B1 = 1, H1 = 2.236067978... . For any value assigned to H1 in this construction, the side B1 is always the hypotenuse times the square root of one-fifth, or H1 * sqrt(0.2), or H1 * 0.447213595... . This is the same as saying that the side B1 is H1 times the cosine. This is what we see in our Similar Right Triangle table: if H = X, then B = X * Cosine.

Therefore, we complete our division by five (or multiplication by one-fifth) when we construct the tangent=2 right triangle again with the length of our second Hypotenuse H2 marked off as equal to the length of Base B1. The length of our new Base B2 is again 0.447213595... times H2, which equals H1 times one-fifth.

This procedure for dividing by 5, therefore, entails construction of a first tangent=2 right triangle with the current value as the line length of the first hypotenuse, and then construction of a second tangent=2 right triangle with the base B value from the first tangent=2 right triangle being the hypotenuse of the second tangent=2 right triangle.

The Tan Two Twice construction:

Construction #10, construction of 0.7778 in 20 steps:

From --------> 0.809016994374947424102293417182819... --> - (2/5)

1) From the line length of 0.809016994374947424102293417182819..., use the compass to subtract the line length of two times B2, whereas B2 = one-fifth of UN. The resulting current line length is 0.409016994374947424102293417182819...

-0.4 = -------> 0.409016994374947424102293417182819... --> *5

2) Use the straightedge to construct a line of suitable length and mark off with the compass the line length of 0.409016994374947424102293417182819... five times. The current line length is now 2.0450849718747371205114670859141... .

*5 = ---------> 2.0450849718747371205114670859141... --> * 2

3) Use the straightedge and compass to construct a line that is two times the length of the current line [2.0450849718747371205114670859141...]. That line times 2 equals

4.09016994374947424102293417182819..., now the current line.

*2 = ---------> 4.09016994374947424102293417182819... --> -3.2 [16/5]

4) Use the straightedge and compass to construct a line that has a length of 3.2, or 16/5, which is equal to 3 times UN plus B2. Then, use the straightedge and compass to subtract that line length of 3.2 from 4.09016994374947424102293417182819..., resulting in a new current line length of 0.890169943749474241022934171828191... .

-3.2 = -------> 0.890169943749474241022934171828191... --> *5

5) Use the straightedge and compass to construct a line that has a length that is five times the length of the current line [0.890169943749474241022934171828191...], resulting in a new current line length of 4.45084971874737120511467085914095... .

*5 = ---------> 4.45084971874737120511467085914095... --> *2

6) Use the straightedge and compass to double the length of the current line length, resulting in a new current line length of 8.90169943749474241022934171828191... .

*2 = ---------> 8.90169943749474241022934171828191... --> (-8.1) in two steps

7) Use the straightedge and compass to subtract a line length of 3.6, or (18/5), or (3 times UN plus 3 times B2) from 8.90169943749474241022934171828191... .

The new current line length is 5.30169943749474241022934171828191...

-3.6 = --------> 5.30169943749474241022934171828191...

8) Use the straightedge and compass to subtract a line length of 4.5, or (4 times UN plus UN/2) from 5.30169943749474241022934171828191... .

The new current line length is 0.801699437494742410229341718281906... .

-4.5 = --------> 0.801699437494742410229341718281906... (-3.6, -4.5) = -8.1

then... -------> 0.801699437494742410229341718281906... --> +4

9) Use the straightedge and compass to add a line length of 4 times UN

to 0.801699437494742410229341718281906...

The new current line length is 4.80169943749474241022934171828191... .

+4 = ---------> 4.80169943749474241022934171828191... --> /5

10) Use the straightedge and compass to perform the Tan Two Twice construction to divide line 4.80169943749474241022934171828191... by 5.

The new current line length is 0.960339887498948482045868343656381... .

/5 = ----------> 0.960339887498948482045868343656381... --> /2

11) Use the straightedge and compass to divide the current line length in half, that is,

0.960339887498948482045868343656381... divided by 2.

The new current line length is 0.480169943749474241022934171828191... .

/2 = ----------> 0.480169943749474241022934171828191... --> +5, + 4 = +9

12) Use the straightedge and compass to add a line length of 9 times UN to the current

line length of 0.480169943749474241022934171828191... --->(when printed, p. 35)

+9 = ---------> 9.48016994374947424102293417182819... --> /5, /2 = /10

13) Use the straightedge and compass to perform the Tan Two Twice construction to divide line length 9.48016994374947424102293417182819... by 5.

The new current line length is 1.89603398874989484820458683436564... .

/5 = ----------> 1.89603398874989484820458683436564... --> /2

14) Use the straightedge and compass to divide the current line length in half, that is,

1.89603398874989484820458683436564... divided by 2.

The new current line length is 0.948016994374947424102293417182819... .

/2 = ----------> 0.948016994374947424102293417182819... --> +4

15) Use the straightedge and compass to add a line length of 4 times UN to the current

line length of 0.948016994374947424102293417182819... .

+4 = ---------> 4.94801699437494742410229341718282... --> * 2

16) Use the straightedge and compass to double the current line length.

4.94801699437494742410229341718282...

*2 = ---------> 9.89603398874989484820458683436564... --> - [sqrt(1.25) +1]

then ---------> sqrt(5)/2 = 1.11803398874989484820458683436564...,

16) Construct the tangent=2 right triangle with the designated unit length UN as the line length for the Base B. The Hypotenuse is sqrt(5) [2.236067978... in proportion to UN.

Use the compass and straightedge to divide the Hypotenuse in half. Therefore,

sqrt(5)/2 = sqrt(1.25) = 1.11803398874989484820458683436564...

17) Use the straightedge and compass to construct a line length of UN plus

1.11803398874989484820458683436564...

+1 = ---------> 2.11803398874989484820458683436564...

then...

19) Use the compass and straightedge to subtract 2.118033988... from 9.896033988...

----------------> 9.89603398874989484820458683436564...

- 2.11803398874989484820458683436564...

= ------------> 7.778 (a "terminal digital value") the current and target line length.

then...

20) 7.778 / 5 = 1.5556, and 1.5556 / 2 = 0.7778, and 1 - 0.7778 = 0.2222

Also, (2 - 0.7778) = 1.2222, (1 + 0.7778) = 1.7778 and so forth.

Here, the observant reader and geometer will see that we can readily construct line lengths of 2.222, and 1.222 and 0.1222, and 0.8778 and 8.778, which can be used for alternative constructions of MQ. I leave it up to the reader to imagine and try the effective steps to get these additional line lengths. Sequential shaping is, I believe, the means by which Nature, together with "sequential halving," creates all the shapes we see, including the shapes of molecules, tissues, and organisms.

--> TOC [Back to VALCON TOC]

The Definition of M and MQ, (MQ = M^2):

Printed below is the relevant output of my computer program XQ1oXQ01, which represents X^2 + (1 over X^2) because Phi belongs to that set of numbers X, such that X^2 plus (1/X^2) = N, an integer greater than 2; because there is no X such that X^2 plus (1/X^2) equals 1 or 2.

Based on a helpful observation made by a friend I have corrected the definition of MQ. I previously interpreted MQ as a variation of MQ+(1/MQ) = the integer 2 exactly. The true value of MQ+(1/MQ) is 2.000000000234... or 2 point followed by nine zeros, subject to greater accuracy that might be found with a high precision computer. The proper definition of MQ is strictly the result of the construction steps described in Values and Constructions Required.

For [X^2 + (1/X^2)] = 2 exactly, X = 1 exactly. The mathematical proposition, and physical proposition is based in part on the concept that physical Pi is variable and depends on the number of sides of a regular polygon, and on the concept that infinite Pi does not exist in the real physical universe. Therefore, construction of MQ enables construction of Pi to the ninth decimal place, which is a precisely accurate value for physical Pi when a regular polygon has 262,144 sides. The SF solution presented here I therefore claim is the best solution proposed to be the solution sought from a Pythagorean student, or candidate, in response to the original riddle. The geometry and understanding of Proportion practiced by the Pythagoreans is the equivalent of modern fractal geometry and chaos theory, and is the origin of shapes and structures, and is in effect the origin of evolution. Evolution is the origin of species and Proportion is the origin of the self-organization of matter.

The significant characteristics of this set are based on the principle that the original Pythagorean Theorem and quadratic equation were neither devised nor used to solve algebraic "problems" in mathematics. They originated centuries before the development of the mathematical practice that we call "algebra," and their original use was for geometric constructions. Therefore, I claim that the quadratic equation was originally, and still is of course, the Quadratic Construction. This is illustrated in greater detail later, under What is Proportion, really?

The Quadratic Construction means that we do not view the equation as an algebraic formula to solve problems. When the quadratic equation is used to solve mathematical problems, we often get a "minus" solution. There is often a minus and a plus solution, and sometimes two plus solutions, but always two solutions. We often get a minus solution that does not constitute a sensible solution. So, in practice, we drop the negative solution and joyfully accept the positive solution as correct. That's fine. However, when we use the quadratic equation as the quadratic construction, all number values are either ratios or line lengths, and in fact we are using the quadratic construction to construct line lengths that have certain significant characteristics. For example, the quadratic construction enables us to construct line lengths of great decimal precision that are exact inverses of one another. The most important reality to recognize about the quadratic construction, in order to understand its original and very powerful meaning, is that because all number values are constructible line lengths, there are really no minus values. This is true for the simple reason that there is no such thing as a minus line length. In reality, in Nature, when we "subtract" a length of 5 from a length of 2, what we are really doing is comparing the two line lengths or "laying" the length of 5 over the length of 2. What we get could be called, mathematically, minus 3, but in reality and in Nature it has to be just 3, always a "plus" value for the line length. If this is still difficult, just think as the 2 minus 5 as having a real concrete result. It is 3, or plus 3, because anything that is physically real has to be "plus" for "present," and it cannot be "minus" for "not present." This is why I make my little joke, a most cosmically serious joke, that...

"There are no minus cows in the real universe."

Contemplate the Quadratic (Equation) Construction.

-b +/- (sqrt[ b^2 - (4*a*c)] ) / 2a = -(b / 2a) +/- ( sqrt[ b^2 - (4*a*c)] ) / 2a )

The values assigned to a, b, and c, and the results of the constructions, are values that will result in two solutions that can still be called the Negative solution and Positive solution. In this printout we are looking at the Negative solution (Neg sol). Why do I call it the Negative solution?

The quadratic construction can be "spelled out" differently, to give two solutions, as:

1) -(b / 2a) + ( sqrt[ b^2 - (4*a*c)] ) / 2a), and...

2) -(b / 2a) - ( sqrt[ b^2 - (4*a*c)] ) / 2a)

The second construction is the Negative solution:

2) -(b / 2a) - ( sqrt[ b^2 - (4*a*c)] ) / 2a) is the Negative solution, because we have a minus sign assigned to the value of both elements:

sqrt[ b^2 - (4*a*c)] ) / 2a, as well as to (b / 2a)

I call that part of the equation that we "get the square root of, "sqrt[ b^2 - (4*a*c)], the "determinant." In the program printout below, it is the first value shown, in brackets. For example: 1) [sqrt(5.000000)]..., because b = sqrt(1).

We do not want to struggle with getting the square root of a negative value (because there are none among line lengths). Therefore, we give "c" the value of (-1) in the program so that the determinant is always positive: sqrt[ b^2 + (4* a * [1] )]

We also assign the value of 1 to "a." Therefore:

-(b / 2a) = -(b/2) and ----> sqrt[ b^2 + (4* a * [1] )] /2a = sqrt[ b^2 + (4* a * [1] )] / 2

You can see now, quite readily, that when we vary the value of b only, and only as the square root of an integer, and begin with 1, we get:

1) -(1/2) + (sqrt[ 1 + (4 *1 *1)] ) /2), and---> -(1/2) - (sqrt[ 1 + (4 *1 *1)] ) /2)

= -0.5 + 1.118033988..., and-----> -0.5 - 1.118033988...

= 0.618033988... (Positive solution) and 1.618033988... (Negative solution)

Because there are no minus line lengths.

The two minus signs accomplish addition of the two line lengths.

And we discover that the Negative solution is X, such that X^2 + (1/X^2) = 3

And the same pattern applies to 2), meaning b = square root of 2, and X^2 + (1/X^2) = 4, and so on, for every integer greater than 2. We also see that our set produced by the quadratic construction begins with 3, not 2. Where is the X, such that X^2+(1/X^2) = 2? It is hidden. This is why I call it the "Holy Ghost." You may understand why I would call it "Ghost," but not "Holy." That is explained under the topic of "The World's Oldest Theological Dispute: The Hiram Key," in Volume 8 Table of Contents.

It is also more or less obvious that we can use this reality to construct all of these values, because all we have to do is construct the square root of the integer to get our "b," and then divide that root "b" by 2 and the determinant root by 2, and then "add" and "subtract" the lines according to the equation. We then square the line X (Negative solution) and line 1/X. The final results give us the four lines (and ratios) of X and 1/X, and X^2 and (1/X^2), such that [X^2 + (1/X^2)] = b squared plus 2. Each line X is absolutely a member of the set of [X^2 + (1/X^2)] = N, N being an integer greater than 2.

When M=X and X=1, then [X^2 + (1/X^2)] = 2 exactly.

Computer program "XQ1oXQ01" printed output follows:

XQ1oXQ01.cpp X+(1/X), X^2+(1/X^2) set (11/30/2006):

1) [sqrt(5.000000)] Neg sol= 1.618033988749895

Neg/Pos+> -sqrt(1.000000000000)/2 -/+sqrt(5.000000000000)/2

1.618033989+0.618033989 2.618033989+0.381966011

* NS+(1/NS)= 2.236067977500 NQ+(1/NQ)= 3.000000000000

2) [sqrt(6.000000)] Neg sol= 1.931851652578136

Neg/Pos+> -sqrt(2.000000000000)/2 -/+sqrt(6.000000000000)/2

1.931851653+0.517638090 3.732050808+0.267949192

* NS+(1/NS)= 2.449489742783 NQ+(1/NQ)= 4.000000000000

3) [sqrt(7.000000)] Neg sol= 2.188901059316734

Neg/Pos+> -sqrt(3.000000000000)/2 -/+sqrt(7.000000000000)/2

2.188901059+0.456850252 4.791287847+0.208712153

* NS+(1/NS)= 2.645751311065 NQ+(1/NQ)= 5.000000000000

4) [sqrt(8.000000)] Neg sol= 2.414213562373095

Neg/Pos+> -sqrt(4.000000000000)/2 -/+sqrt(8.000000000000)/2

2.414213562+0.414213562 5.828427125+0.171572875

* NS+(1/NS)= 2.828427124746 NQ+(1/NQ)= 6.000000000000

5) [sqrt(9.000000)] Neg sol= 2.618033988749895

Neg/Pos+> -sqrt(5.000000000000)/2 -/+sqrt(9.000000000000)/2

2.618033989+0.381966011 6.854101966+0.145898034

* NS+(1/NS)= 3.000000000000 NQ+(1/NQ)= 7.000000000000

6) [sqrt(10.000000)] Neg sol= 2.805883701475779

Neg/Pos+> -sqrt(6.000000000000)/2 -/+sqrt(10.000000000000)/2

2.805883701+0.356393959 7.872983346+0.127016654

* NS+(1/NS)= 3.162277660168 NQ+(1/NQ)= 8.000000000000

7) [sqrt(11.000000)] Neg sol= 2.981188050709995

Neg/Pos+> -sqrt(7.000000000000)/2 -/+sqrt(11.000000000000)/2

2.981188051+0.335436740 8.887482194+0.112517806

* NS+(1/NS)= 3.316624790355 NQ+(1/NQ)= 9.000000000000

8) [sqrt(12.000000)] Neg sol= 3.146264369941973

Neg/Pos+> -sqrt(8.000000000000)/2 -/+sqrt(12.000000000000)/2

3.146264370+0.317837245 9.898979486+0.101020514

* NS+(1/NS)= 3.464101615138 NQ+(1/NQ)= 10.000000000000

9) [sqrt(13.000000)] Neg sol= 3.302775637731995 --->(when printed, p. 40)

Neg/Pos+> -sqrt(9.000000000000)/2 -/+sqrt(13.000000000000)/2

3.302775638+0.302775638 10.908326913+0.091673087

* NS+(1/NS)= 3.605551275464 NQ+(1/NQ)= 11.000000000000

10) [sqrt(14.000000)] Neg sol= 3.451967523471160

Neg/Pos+> -sqrt(10.000000000000)/2 -/+sqrt(14.000000000000)/2

3.451967523+0.289689863 11.916079783+0.083920217

* NS+(1/NS)= 3.741657386774 NQ+(1/NQ)= 12.000000000000, and so forth.

It may be that there is a way to use the quadratic construction to construct M and MQ, but if there is, I have not yet discovered that procedure. In any case, M, being the square root of MQ, "almost" belongs to this set of numbers because MQ + (1/MQ) = 2.000000000234... but not 2 exactly. To construct the value MQ, or a value very close to MQ, we have to do just six more constructions.

I want to comment also that I know as many do that for centuries individuals have worked hard to calculate the value of Pi to more and more decimal digit places. It is my understanding that modern, highly precise computers have calculated the decimal value of Pi to hundreds of places, then thousands of places, and possibly more than a million places. This exercise is supposedly to show, or cast in doubt, that there is no repeated pattern of digits and Pi is indeed an "endless non-repeating decimal." You can now add M and MQ to your list of "endless non-repeating decimals" to be computed in this same way. MQ = 1 / [Pi (your Pi or mine) * (phi^2) * (5/6)].

Therefore, this is also the definition of MQ:

End of definition of MQ.

The Construction of TN and NT:

Look back at Construction #4. The tangent is (9/11) or 0.818181818...

Look back at Construction #9-4. The length of Altitude A9-4 is equal to the secant of 18 degrees raised to the fourth power, or 1.222291236... in proportion to our UN (one).

Construction # 11: (Construction of TN and NT in two steps)

With the straightedge and compass, re-construct right triangle # 4, with the tangent of (9/11), but make the length of the Base B11-1 equal to the length of Altitude A9-4 (1.222291236...). The length of Altitude A11-1 is now 1.000056466... in proportion to UN, and this is TN. Repeat: Construct perpendiculars, mark off length B11-1 (equal to the line length of 1.222291236..., from Construction #9-4) to the right of the intersection of the perpendiculars. At the right end point of Base B11-1 re-construct the angle G from Construction #4 [tangent = (9/11)]. The extended upper side of the similar constructed angle is the Hypotenuse H11-1. Side A11-1 = 1.000056466..., which I call "TN."

Construction #11-1, Step 1:

Facts for Right Triangle #11-1:

A11-1 = 1.000056466..., B11-1 = 1.222291236..., H11-1 = 1.57927477...

G = 39.28940686..., OPP = 50.71059314...

Sine = 0.63323779..., Cosecant = 1.5791856...

Cosine = 0.773957299..., Secant = 1.292060946...

Tangent = 0.818181818..., Cotangent = 1.222222222...

Construction #11-2, Step 2:

With the straightedge and compass, construct perpendiculars, make Base B11-2 equal to the length of TN (1.000056466...) and the length of A11-2 equal to UN. With the straightedge, construct the Hypotenuse H11-2 between the end points of the Altitude and Base. The tangent of right triangle #11-2 is (1/TN) or NT = 0.999943537... .

The drawing for Construction #11-2 is not to scale. The difference between 1 and 1.000056466... is not visible and this is a key point about this entire process of squaring the circle. The constructed values are of such fine precision, that the challenge is not to see the differences in physical line lengths, but to see that the constructions embody the calculations that lead to the end result: the identification of M and squaring the circle in terms of number values, even though the differences in physical line lengths are not visible. This fact is proof, in my opinion, that the ancients knew this is the correct answer to the original riddle about squaring the circle. They knew the values of Pi, Phi and M to a sufficient level of precision to know that construction of MQ enables squaring the circle.

Facts for Right Triangle #11-2:

A11-2 = UN (1), B11-2 = TN = 1.000056466..., H11-2 = 1.41425349...

G = 44.99838242..., OPP = 45.00161758...

Sine = 0.707086817..., Cosecant = 1.41425349...

Cosine = 0.707126774..., Secant = 1.414173638...

Tangent = 0.999943537..., Cotangent = 1.000056466...

We now have the ratio, and line length, of NT = 0.999943537..., which we are going to use to construct the value of MQ. There is more than one procedure that gives the same result. I believe there are probably some procedures for constructing MQ and or M that I have not yet discovered. You can search for these yourself, if you are as fascinated by Proportion as I am.

--> TOC [Back to VALCON TOC]

The Construction of MQ and M (Constructions #12, #13, #14, #15, and 16):

First note that: NT = 0.999943537369751504522585249236876...

and SF = 1.22229123600033648574532213002996... = (secant 18)^4

These two values enable us to construct MQ, which is "written" by my desktop calculator in two ways:

1) As: MQ = 1.00001532123408073944164930824006...

When constructed as shown here, and as can be constructed in more than one way.

2) As: MQ = 1.00001532118112944385403915398333...

When calculated as a factor of Phi^2, meaning use the desktop calculator to first write the value of Phi^2 [2.61803398874989484820458683436564...], then divide that value by Pi and then divide by (5/6) or multiply by 1.2.

Compare the two calculated values, which should be exactly the same, and you can see that the difference appears following the 9th decimal digit. This is because a desktop computer calculator is not precise, or not precisely correct, beyond the 9th or 10th decimal place. You might ask, then, if...

1) MQ#1 = 1.000015321--23408073944164930824006..., and

2) MQ#2 = 1.000015321--18112944385403915398333...

How do I know that MQ is valid? How do I know that there is one valid precise value for MQ, an endless non-repeating decimal, just as there is one valid precise value for Pi, an endless non-repeating decimal? The reason I am certain MQ is valid as I have defined it is because of hundreds of other calculations I have made that are too numerous and tedious to show here, and which probably would not convince anyone anyway because they were all made on a desktop computer. The only final test is a test that can be run by anyone who has access to a more precise computer calculator. The kinds of tests are spelled out -- the descriptions are just a few sentences -- under "How the validity of my work can be tested with a super-computer."

Looking at our two values again, both of which have been constructed already:

NT = 0.999943537369751504522585249236876... (Construction #11)

SF = 1.22229123600033648574532213002996... = SF = (secant 18)^4 (#9-4)

The calculation to be performed by construction:

For our next construction, we are going to construct a new value, NTP, using only the value of NT. NTP = 0.999937891425529516432675419924049... . Our constructions will perform the calculation of:

NT + 9 = 9.999943537369751504522585249236876..., then divide by 2, and by 5, or,

we will see that we can divide a long line first by 4, then by 5, then multiply by 2:

= 0.9999943537369751504522585249236876..., intermediate value. Then that * NT

= 0.999937891425529516432675419924049... = NTP

Then, NTP * SF = 1.22221532123408073944164930824006... (target value).

Construction #12 (six steps, to get NTP value [0.999937891...])

NT + 9 = 9.999943537369751504522585249236876..., then divide by 2, and by 5, or,

we will see that we can divide this line first by 4, then by 5, then multiply by 2:

= 0.9999943537369751504522585249236876..., intermediate value. Then that * NT

= 0.999937891425529516432675419924049... = NTP

Then, NTP * SF = 1.22221532123408073944164930824006..., most interesting, because MQ = 1.00001532123408073944164930824006... .

1) With compass and straightedge, add 9 * UN. Our current line length now is equal to

9.999943537369751504522585249236876..., which would just fit on a standard sheet of paper in the "landscape" orientation.

2) With compass and straightedge, divide our current line in half. Our line now equals

4.99997176868487575226129262461844...

3) With compass and straightedge, divide our current line in half. Our line now equals

2.49998588434243787613064631230922...

4) Next divide the current line by 5 using the "Tan Two Twice" method. Our current line length is now: 0.499997176868487575226129262461844...

5) Using the compass and straightedge, multiply our current line length by 2 (double it). We have reached our target intermediate value. Our current line length is now:

0.999994353736975150452258524923688..., which is not NT. Our current line length begins with 5 decimal nines, not four.

6) Next, with compass and straightedge, re-construct our right triangle with the tangent equal to NT. That is the right triangle of Construction #11-2. And make the line length of Base B12 our current line length of 0.999994353736975150452258524923688... . Repeat: Construct perpendiculars. Mark off the line length of the Base B12, to the right of the intersection of the perpendiculars, equal to our current line length, which is the value with 5 decimal nines [0.999994353736975150452258524923688...]. At the right end point of B12, re-construct the angle from Right Triangle #11-2 (tangent = NT = 0.999943537...). The extended upper side of this similar angle is the Hypotenuse H12.

Since Altitude A12 will be B12 times the tangent (NT), we have completed construction of our target value NTP. Altitude A12 equals NTP, and that value, our current line length, is 0.999937891425529516432675419924049...

Facts for Right Triangle #12:

A12 = 0.999937891425..., B12 = TN = 0.999994353736...(5 nines),

H12 = 1.414165653...

G = 44.99838242..., OPP = 45.00161758...

Sine = 0.707086817..., Cosecant = 1.41425349...

Cosine = 0.707126774..., Secant = 1.414173638...

Tangent = 0.999943537..., Cotangent = 1.000056466...

Construction #13: (to get tangent = 1.222291236...)

For Construction #13, we begin by looking back at Construction #9-4:

Review of Right triangle #9-4: (to get line/ratio = 1.222291236...)

A9-4 = 1.222291236..., B9-4 = 1.162468045..., H9-4 = 1.686809954...

G = 46.4369994..., OPP = 43.5630006...

Sine = 0.72461704..., Cosecant = 1.38003931...

Cosine = 0.689151757..., Secant = 1.451059202...

Tangent = 1.051462224, Cotangent = 0.951056516...

Line A9-4 is established as (secant 18)^4, or 1.222291236..., in proportion to UN. Therefore, use the compass and straightedge to construct a right triangle with Altitude A13 equal to A9-4 (1.222291236...) and Base B13 equal to UN. Construct perpendiculars, then mark off the lengths of A13, and B13. Use the straightedge to construct the Hypotenuse H13 between the end points of A13 and B13.

Facts for Right Triangle #13:

A13 = 1.222291236..., B13 = 1 (UN), H13= 1.579239015...

G = 50.71217868..., OPP = 39.28782132...

Sine = 0.773974822..., Cotangent = 1.292031693...

Cosine = .633216372..., Secant = 1.579239015...

Tangent = 1.222291236..., Cotangent = .818135621...

Construction #14: ( to get 1.22221532123408073944164930824006... [MQ+0.2222])

With the compass and straightedge, re-construct Right Triangle #13 and make the length of Base B14 equal to NTP (0.999937891425529516432675419924049...). Construct angle G from Right Triangle #13 with the vertex pointing to the right. Mark off the length of Base B14 from the vertex to a point on the base line to the left of the vertex.

Construct a perpendicular at the left end point of Base B14. The length of Altitude A14 will then be NTP * Tangent (1.222291236...), which is equal to our target value.

Our line length for A14 is: 1.22221532123408073944164930824006... !

Facts for Right Triangle #14:

A14 = 1.22221532123408073944164930824006...

B14 = 0.999937891425529516432675419924049...

H14= 1.57914093043270245952072874499882...

G = 50.71217868..., OPP = 39.28782132...

Sine = 0.773974822..., Cotangent = 1.292031693...

Cosine = .633216372..., Secant = 1.579239015...

Tangent = 1.222291236..., Cotangent = .818135621...

Construction #15: (final construction to get MQ)

For Construction #15, which involves only line lengths, look back at Construction #10, and step 20 for that construction:

[Step] 20) 7.778 / 5 = 1.5556, and 1.5556 / 2 = 0.7778, and 1 - 0.7778 = 0.2222

We see that we have constructed line length 0.7778, and line length 0.2222.

Therefore, with the compass and straightedge, subtract line length 0.2222 from our line length from Construction #14 (1.22221532123408073944164930824006...). Line shown for this simple procedure, which means, in construction and calculation:

____________ minus __ = __________

However, note also that [(NT+9)/10]*NT = ( NT^2 + [9*NT] ) / 10 = NTP, and

A second calculation of MQ that can be performed by construction:

Note that NT * (11/9) = 1.22215321234080739441649308240063...

or, 0.999943537369751504522585249236876...

* 1.22222222222222222222222222222222...

= 1.22215321234080739441649308240063..., and this value, minus 0.222

= 1.00015321234080739441649308240063..., and this value, plus 9

= 10.00015321234080739441649308240063..., and this value, /5, /2

= 1.000015321234080739441649308240063..., our MQ, which calculations can be performed by construction.

A third calculation of MQ that can be performed by construction:

Recall that NTP = 0.999937891425529516432675419924049..., then begin with

(sec 36)^2: 1.52786404500042060718165266253745... [= (0.763932022...*2)]

* 4 = 6.11145618000168242872661065014979...

* NTP [ 0.999937891425529516432675419923174...]

= 6.11107660617040369720824654120001...

/5 = 1.22221532123408073944164930824006...

A fourth calculation of MQ that can be performed by construction:

(NT)^2 [0.999887077927531623623486956108611...]

* SF [(secant 18)^4] []

= 1.22215321234080739441649308240063...

A fifth calculation of MQ that can be performed by construction:

NT * (secant 18)^2 [1.10557280900008412143633053250749...]

= 1.10551038545135675917362375494506...

square root of = 1.22215321234080739441649308240063...

A sixth calculation of MQ that can be performed by construction:

In Construction #12, our "intermediate value" is 0.9999943537... (with 5 decimal nines). We then multiply that by NT (0.999943537...) to get our NTP value (0.999937891...). But, we can see that NT times (secant 18^4) [1.222291236...] equals (11/9) [1.222222222...]. Therefore, (11/9) times our "intermediate value" of 0.9999943537... also is equal to 1.222215321... .

Construction #16: [final construction to get MQ and M:

Construct a rectangle with height H = 1 (UN) and length L = MQ. Square the rectangle. See previous description of squaring-the-rectangle, if necessary. The side of the square constructed in the squaring-the-rectangle procedure is deemed to equal, of course, the square root of MQ, or M, which is: 1.00000766058769806778093094275226..., and M^2 = MQ.

--> TOC [Back to VALCON TOC]

The Get Pi constructions: (Constructions #17 through #20)

At this point the reader is free to believe, or suspect, that my claim for constructing MQ here, as defined, is only theoretical until proven with one of the most accurate computers available. That is understood and accepted. Let us proceed all the way to constructing squares and circles exactly equal in area.

Construction #17, in two steps:

Construction #17-1: (to get ratio of 1.618033989...)

We see that in our first construction, the right triangle to the left of the tangent = 2 right triangle (the start of the pentagon construction), has a tangent of Phi (1.618033989...). We could use that ratio to construct the line length, but we already have constructed a line length of Phi/2 (in proportion to UN) with our Construction #10 right triangle, the right triangle that has the Base side equal to the cosine of 36 degrees: 0.809016994... .

Take the line length of 0.809016994... from Construction #10 and double it. That is our line length of 1.618033989... in proportion to UN. Now we construct perpendiculars, and to complete our Right Triangle #17-1, we mark off the length of 1.618033989... as the length of Altitude A17-1, and then mark off, to the right of the perpendicular intersection, the length of UN as the length of Base B17-1. With the straightedge, construct the Hypotenuse H17-1 between the end points of A17-1 and B17-1.

Facts for Right Triangle #17-1:

A17-1 = 1.618033989..., B17-1 = UN (1)

H17-1 = 1.902113033... sqrt(3.618033989...) = (cosine 18)*2

G = 58.28252559..., OPP = 31.71747441...

Sine = 0.850650808..., Cotangent = 1.175570505...

Cosine = 0.525731112..., Secant = 1.902113033...

Tangent = 1.618033989..., Cotangent = 0.618033989...

Construction #17-2: (to get line length of Phi^2)--->(when printed, p. 50)

Re-construct Right Triangle #17-1, with a Base B17-2 equal to Phi. Construct perpendiculars. Mark off the line length of Phi as the length of Base B17-2, to the right of the perpendicular intersection. At the right end point of Base B17-2, re-construct the acute angle (G) for this right triangle similar to #17-1. The extended upper side of that angle becomes the hypotenuse H17-2, and the length of our Altitude, A17-2, is now equal to the line length of Phi squared (2.618033989...).

Facts for Right Triangle #17-2:

A17-2 = 2.618033989..., B17-2 = 1.618033989...

H17-2 = 3.077683537... sqrt(9.472135955...) = (cotangent 18)

G = 58.28252559..., OPP = 31.71747441...

Sine = 0.850650808..., Cotangent = 1.175570505...

Cosine = 0.525731112..., Secant = 1.902113033...

Tangent = 1.618033989..., Cotangent = 0.618033989...

Construction #18: (to get tangent = [Pi*(5/6)] )

Construct perpendiculars. To the right of the perpendicular intersection, mark off the line length of our constructed MQ length (which is MQ in proportion to UN) as the length of Base B18. With the compass, mark off the length of Phi^2, the length of A17-2, as the length of our current Altitude B18. With the straightedge, construct the Hypotenuse H18 between the end points of A18 and B18. The tangent of Right Triangle #18 is equal to Pi times (5/6) (2.617993878...).

Facts for Right Triangle #18:

A18 = 2.618033989..., B18 = MQ, H18 = 2.802522544... = sqrt(7.854132609...)

G = 69.09454994..., OPP = 20.90545006...

Sine = 0.934170536..., Cotangent = 1.070468358...

Cosine = 0.35682686..., Secant = 2.802479606...

Tangent = 2.617993878..., Cotangent = 0.381971863...

Construction #19: (to get line length [Pi*(5/6)] )

Re-construct Right Triangle #18, with a base length of 1. Construct perpendiculars. Mark off the line length of UN, to the right of the perpendicular intersection, as the length of Base B19. At the right end point of Base B19, re-construct the acute angle (G) for this right triangle similar to #18. The extended upper side of that similar angle becomes the Hypotenuse H19, and the length of our Altitude A19 is equal to Pi times (5/6).

Facts for Right Triangle #19:

A19 = 2.617993878..., B19 = UN (1), H19 = 2.802479607... = sqrt(7.853891945...)

G = 69.09454994..., OPP = 20.90545006...

Sine = 0.934170536..., Cotangent = 1.070468358...

Cosine = 0.35682686..., Secant = 2.802479606...

Tangent = 2.617993878..., Cotangent = 0.381971863...

Obviously, the physical difference between Right Triangle #18 an Right Triangle #19 is not visible to the human eye. It is visible to the Eye of Ra, which sees all things both great and small.

Construction #20: (in two steps, to get line length of Pi)

Construction #20-1:

Reminder that constructing line length of Pi means we can also readily construct the ratio equal to Pi. We see that at Construction #3 we have a line length of 1.2 (6 * B2) in proportion to UN. For Right Triangle #20-1, we simply construct perpendiculars, mark off (to the right) the Base B20-1 as line length UN, and the Altitude A20-1 as line length 1.2 (our UN + B2), and then construct the Hypotenuse H20-1 between the end points of A20-1 and B20-1. Right Triangle #20-1 has a tangent of 1.2 or (6/5).

Facts for Right Triangle #20-1:

A20-1 = UN+B2 (1.2), B20-1 = UN (1), H20-1 = 1.562049935... = sqrt(2.44)

G = 50.19442891..., OPP = 39.80557109...

Sine = 0.768221279..., Cotangent = 1.301708279...

Cosine = 0.640184399..., Secant = 1.562049935...

Tangent = (6/5), Cotangent = (5/6)

Construction #20-2: (to get the line length of Pi)

Re-construct Right Triangle #20-1, but with a base line length of [Pi *(5/6)]. Construct perpendiculars. Mark off the line length of [Pi*(5/6)], our line length A19, to the right of the perpendicular intersection, as the length of Base B20-2. At the right end point of Base B20-2, re-construct the acute angle (G) for this right triangle similar to Right Triangle #20-1. The extended upper side of that similar angle becomes the Hypotenuse H20-2, and the length of our Altitude A20-2 is equal to Pi. Altitude A20-2 equals Base B20-2 [Pi * (5/6)] times the tangent (6/5). We have constructed our ultimate target value of Pi in proportion to UN (1).

Facts for Right Triangle #20-2:

A20-2 = 3.141592654..., B20-2 = 2.617993878...,

H20-2 = 4.089437167... = sqrt(1672349635...)

G = 50.19442891..., OPP = 39.80557109...

Sine = 0.768221279..., Cotangent = 1.301708279...

Cosine = 0.640184399..., Secant = 1.562049935...

Tangent = (6/5), Cotangent = (5/6)

--> TOC [Back to VALCON TOC]

The Pi and 1 Constructions: (improved from Volume 1 of Welcome to Aquarius)

The Pi and One Set of Right Triangles: --->(when printed, p. 55)

Construction of Pi and 1 in proportion to one another, enables squaring the circle exactly.

Four Right Triangles, labeled PM, RP, OR, and RE.

Constructing the PM Right Triangle: (to get Right Triangle with Cosine = [(Pi/2)-1])

To construct the PM (Pi Mantissa) right triangle, we construct perpendiculars and then mark off the value of [(Pi/2)-1] as the length of Base B (0.570796326...). Then with the compass open to a distance equal to UN, mark off the length of Hypotenuse H as the line length of 1.

Facts for Right Triangle PM:

A-PM = 0.821091683..., B-PM = 0.570796326..., H-PM = 1

G = 55.194225271..., OPP = 34.805774728...

Sine = 0.821091683..., Cosecant = 1.217890790...

Cosine = 0.570796326794..., Secant = 1.751938393...

Tangent = 1.438502045..., Cotangent = 0.695167589...

Note that the ratios would be exactly the same if we subtracted 2 from 3.141592654... and made Base B-PM = 1.141592654... and Hypotenuse H-PM = 2 instead of 1.

Constructing the RP [(sqRt of Pi) / 2)] Right Triangle: (to get square Root of Pi)

To construct the RP right triangle, we divide the angle G of the PM right triangle in half and use the compass to mark off the line length of 1 for the Hypotenuse H-RP. Then we drop a perpendicular from the upper end point of H-RP to the base line to construct Base B-RP. (See Construction #8 for how to divide an angle in half.)

Facts for Right Triangle RP:

A-RP = 0.463251375..., B-RP = 0.886226925..., H-RP = 1

Angle G = 27.597112635690...,, OPP = 62.402887364...

Sine = 0.463251375..., Cosecant = 2.158655221...

Cosine = 0.886226925..., Secant = 1.128379167...

Tangent = 0.522723200..., Cotangent = 1.913058380...

Note that in the RP right triangle the cosine of sqrt(Pi)/2 [or sqrt(Pi) when doubled] enables us to convert the area of a circle to the area of a square. The ratios for Right Triangle RP would be exactly the same if we made H-RP = 2 instead of 1, and the length of B-RP would then be equal to the square root of Pi (1.772453851...).

Constructing the OR (one Over the sqRt of Pi) Right Triangle: (to get ratio [1/sqrt(Pi)] ).

To construct the OR right triangle, we first construct perpendiculars and then use the compass to mark off, to the right of the perpendicular intersection, the length Base B-OR equal to 1. Then open the compass to the distance of the square root of Pi (from the RP Right Triangle). With the compass, mark off the length of the Hypotenuse H-OR equal to the Square Root of Pi.

Facts for Right Triangle OR:

A-OR = 1.463418140378..., B-OR = 1, H-OR = 1.772453850905...

G = 55.653966546..., OPP = 34.346033453...

Sine = 0.825645271..., Cosecant = 1.211173896...

Cosine = 0.564189584..., Secant = 1.772453851...

Tangent = 1.463418140..., Cotangent = 0.683331696...

Constructing the RE (REverse) Right Triangle: (to get line length [1/sqrt(Pi)] ).

To construct the RE right triangle, we first reconstruct the angle G from the OR right triangle, with the vertex pointing to the right. Then with the compass mark off a line length of 1 for the Hypotenuse H-RE. Then drop a perpendicular from the upper end point of H-RE to the base line. This makes the length of Base B-RE equal to the cosine which is the line length of 1/ sqrt(Pi) or 0.564189584... .

Facts for Right Triangle RE:

A-RE = 0.825645271..., B-RE = 0.564189584..., H-RE = 1

G = 55.653966546..., OPP = 34.346033453...

Sine = 0.825645271..., Cosecant = 1.211173896

Cosine = 0.564189584..., Secant = 1.772453851...

Tangent = 1.463418140..., Cotangent = 0.683331696...

Converting any square area to a circle (S-->C): --->(when printed, p. 60)

Now for any line length N equal to S the side of a square, we can construct a circle with exactly the same area. As an example, let us make N = 1.2 = S. The area of the square is S^2 or 1.44. For the STC construction we reconstruct angle G of the OR right triangle and make the line length of H the length of S, in this case 1.2 . Then we drop a perpendicular from the end point of H to line B. The cosine is 1/ sqrt(Pi) and therefore the length of B in this construction is 1.2 times 1/ sqrt(Pi) = (0.6770275...). We now have a line length B that we can use as the radius of a circle. Using the compass to construct the circle, we see that with a radius R = 0.6770275..., we then have R^2 = 0.458366236... and Pi * R^2 = 1.44 exactly. We can readily make the observation that this algorithm for the use of the OR right triangle is essentially a function that works for any line length N = S the side of the square. [If H=X, B= (H*Cosine)]

Converting any circular area to a square (C-->S):

Now we can also perform the reverse operation of converting the exact area of a circle to a square. For any line length N equal to R the radius of a circle, we can construct a square with exactly the same area. As an example, let us make N = 1.77 = R. The area of the circle is R^2 or 3.1329 times Pi, which equals 9.842295624... . For the CTS construction we reconstruct angle G of the RP right triangle and make the line length of H two times the radius of the circle. Then we drop a perpendicular from the end point of H to B. Two times R (1.77) equals 3.54. Therefore, our side B now equals H * cosine or 3.54 * [sqrt(Pi)/2] = 3.54 * 0.886226925... or the line length value of 3.137243316... We then take that line length with our compass and make it the side of the square, and we then see that the area of the square is 9.842295624... exactly equal to the area of the circle. We can readily make the observation that this algorithm for the use of the RP right triangle is essentially a function that works for any line length N = R the radius of the circle. [If H=X, B= (H*Cosine)]

The Pi and MQ Constructions: (alternative square = circle area)

Without drawings, we can see that the following calculations can be performed as constructions. If we make the radius (RD) of a circle any value sqrt[RX*(5/6)*MQ] for any RX, then RD^2 = [RX*(5/6)*MQ], and RD^2 * Pi = RX*[Pi*(5/6)*MQ], which is equal to RX * Phi^2. We can then construct a rectangle with S1= Phi^2 and S2 = RX, and then square that rectangle, and that square is exactly equal in area to the circle.

A second procedure is to multiply [RX*(5/6)] times the line (Pi*MQ) to get a rectangular area = RX*[Pi*(5/6)*MQ]. Square that rectangle, which of course equals the area of a circle with a radius of sqrt[RX*(5/6)*MQ], or RD = sqrt(RX)*sqrt(5/6)*M.

We can get the value (ratio and line length) of (Pi*MQ) in several ways. One way is to begin with a line length of sqrt(0.8). Make that value the tangent of a right triangle. The cosine is 0.74535592... . The secant is 1.341640786... . Ad 1.8 to the secant of that right triangle to get 3.141640786... = (Pi*MQ).

A second procedure: Phi^2 * 3 = 7.854101966..., * 0.4 = (Pi*MQ).

A third procedure: Phi^2 * Phi^2 = 6.854101966..., plus 1 = 7.854101966... .

A fourth procedure: Phi^2 * sqrt(5) = 5.854101966... .

Now, you might begin to see that there is something going on here, which is what I call the distinct field of study of "Proportion." You may be interested in looking a little further into "What is Proportion, Really?"

A New Definition of Pi:

Looking back at Construction #15, and our sixth calculation of MQ that can be performed by construction, we see that in Construction #12, construction of our "intermediate value" is 0.9999943537... (with 5 decimal nines). We then multiply that by NT (0.999943537...) to get our NTP value (0.999937891...). But, we can see that NT times (secant 18^4) [1.222291236...] equals (11/9) [1.222222222...]. Therefore, (11/9) times our "intermediate value" of 0.9999943537... also is equal to 1.222215321... .

Using these values (others could be used), we can "build" a new definition of Pi:

Pi = Phi^2 / [ (5/6) * MQ ] and then Pi = Phi^2 *(6/5) / MQ

and we have MQ = ( [0.999994353... * (11/9)] - 0.2222 )

therefore: Pi = Phi^2 *(6/5) / ( [0.999994353... * (11/9)] - 0.2222 ), but also:

(A/B) = Phi^2 = tangent 69.0948425521107009670710416347109...

(A/B) = (6/5) = tangent 50.1944289077348059937205101807024...

(A/B) = 0.999994353... = tangent 44.9998382460226753546198632774049...

(A/B) = (11/9) = tangent 50.7105931374996425126958813482344...

(A/B) = 0.2222 = tangent 12.5275943810522240461429804451838...

Therefore, Pi = (tan 69.094842552...)*(tan 50.194428907... ) .

divided by --> [(tan 44.999838246...)*(tan 50.710593137...) ] - (tan 12.527594381...)

Still, all this means is that Phi^2 * 1.2 is the inverse of (phi)^2 * (5/6)

3.141640786...(Pi*MQ) is the inverse of 0.318305009..., and

this too is Proportion, because 1/MQ = Pi * (phi)^2 * (5/6).

BACK LINK: [How to Square the Circle Exactly]

Link to: (Welcome) or (Geometry Alpha Index).