Welcome To Aquarius, Volume 3 (March 6, 2006)
Welcome to Aquarius
, a new journal of informed dissentThe Rediscovery of Proportion: The Secret of Life in the Universe
continued
Volume 3 (March 6, 2006): Medicine and the Polyhedral Atom
Citation suggested: Manimas, John. The Rediscovery of Proportion, "Welcome to Aquarius," Medicine and the Polyhedral Atom, www.jmanimas.com, Volume 3 (March 6, 2006).
To continue interpreting the message of the Great Phi Pyramid, I propose...
1) A Polyhedral Model of the Atom
2) The Living Crystal Electromagnetic Atom (LICEA, lie-see)
3) The Living and the Non-Living God and Nature
4) What is the Most Fundamental Issue of Religion?
5) The Molecular Mirror Method for Identifying an Anti-Virus
6) The Programmable Mathematics of the Molecular Mirror Method
7) Experimental design to address the polyhedral atom issue
8) The Story of Time Tweet
9) The Secret of Life in the Universe
10) The Minus Line Issue
11) The Minus Cow Problem
12) The Reformation of Mathematics and Science
13) The Meaning is That the Pharaoh Points to the Secret of Life
14) The Message From the Ancients: summary of Volumes 1-3 of
The Rediscovery of Proportion: The Secret of Life in the Universe
Link to: (Welcome) or (Geometry Alpha Index) .
########################################################################
1) A Polyhedral Model of the Atom
The atom is not a sphere. The atom has a heartbeat. The atom is alive. The atom is a polyhedron. The atom is a living crystal. This is why snowflakes are crystals and the structure of minerals are crystalline. Salts are crystals and liquids are crystals. Piezzo-electricity is a crystal.
The nucleus vibrates, but this "vibration" is a rhythmic pulse of electromagnetic energy. It pulses for a very short period of time, at very rapid intervals. When it pulses, it captures the electrons for that very short period of time. The electrons travel in straight lines and would leave or escape the vicinity of the nucleus of the atom except for the electromagnetic pulse that captures them for a time interval far less than a nanosecond, and during that very small interval of time, the electron spins rapidly in place, and turns a corner, and this turn forms the vertex in the path of the electron. The electron continues to spin but travels in a straight line for a very short interval, and this brief travel in a straight line forms the side of a polygon and polyhedron that is shaped by the paths of the electrons. The electron therefore, together with the other electrons in its same "orbital set" forms a polyhedral surface that maintains the atom's polyhedron or crystal shape. This model is metaphorically like a neon light that is flickering: ssst, ssst, ssst, ssst. At each "ssst" the electron is captured and held still, and spun, for that very short interval. It turns the "corner," the vertex of the polygonal path, and then travels straight again until the next "ssst." The atom has a heartbeat. The atom is alive.

2) The Living Crystal Electromagnetic Atom (LICEA, lie-see):
The LICEA is consistent with virtually all data we have about atomic and sub-atomic realities.
1) Atoms possess an electrical charge, which creates a cumulative charge when bonded into a specific form of molecule. As stated previously, the "vibrational" signature of each atom is, according to the LICEA theory, a form of electromagnetic charge produced by the nucleus that captures and drives the electron motion in the vicinity of the nucleus.
2) Pure metals are crystalline in structure.
3) Liquids, including water of course, possess a crystalline structure.
4) Organic chemistry tells us that for some reason specific sets of molecules, such as HO and NH and other molecular "parts" that carry a gas or a metal atom can all "latch on" by some generic hook to the carbon atom. This suggests that atomic structure is a kind of "building toy" that enables ready attaching and detaching of molecular parts.
5) Nature has been described rather convincingly, through "chaos theory," as repeating the same patterns on a different scale. Therefore, the fact that much of Nature is crystalline in structure is consistent with this theory that the atom, the basic building block of Nature, possesses a crystalline or polyhedron form.
6) At the sub-atomic level, we have discovered what appears to be many sub-atomic "particles" that often possess a very short interval of time for their "existence." It makes sense that these "particles" are actually varieties of electrical charges. As part of the LICEA theory, I offer an expanded electrical atomic theory: the sub-atomic particles are members of a set of electrical charges. I propose that electromagnetic energy is not comprised simply of positive and negative charges. There is a set of several forms of electrical charges that require more detailed description than simply either "negative" or "positive." This is why we have theories about a "weak force" and a "strong force" at the sub-atomic level. These "forces" are variations of electrical charge. We need to think about a set of electrical charges and not just an opposing pair. The opposing pair of charges may in fact be appropriate for "magnetism," but not for "electromagnetism."
7) Human brains often miss the correct perception of reality by making things more complicated than they are. This viewpoint is described in greater detail in "The Story of Time Tweet."
3) The Living and the Non-Living God and Nature:
During the twentieth century, scientists conducted experiments and research directed toward the specific purpose of discovering how non-living matter becomes living matter. This search has involved various statements about what distinguishes what is alive from what is not alive. Historically, and in somewhat childlike terms, we first would think of mobility as the distinguishing characteristic. That is, living things can move on their own. Dead things do not move. However, this is not necessarily true, because objects that we have labeled as non-living, such as stones or water, do move. A closer look told us that the special characteristic of living things was their organization. That still did not seem satisfactory in itself. For a time, a fairly popular theory of life was that growth was the essential characteristic of life. If it grew, it was alive. If it did not grow, it was not alive. This also did not seem fully satisfactory. There still was something more. In the middle of the century, the double helix of DNA was discovered and identified as a key to understanding what occurred inside living cells and how DNA and RNA played the major roles in genetic reproduction. Toward the end of the twentieth century, studies in the field of medicine, such as the studies of viruses and the human immune system, and studies of biology and the origin of life converged to some degree. During this period of the second half of the century, it became widely accepted by scientists, and popularized, that the essential quality of living matter at the cellular level is that it is self-organizing and self-replicating. This self-organizing ability has intrigued scientists and the interested public for decades, and some scientists have proposed a small variety of theories as to when and how non-living matter becomes self-organizing. It has been proposed, for example, that the self-organizing quality of certain types of organic molecules start in a form of ancient sea, or "primordial soup," but that a stroke of lightning or some similar form of electromagnetic energy needs to be "injected" into the matter in order to change it and convert it to self-organizing, living molecules. Another theory proposes that certain types of clay molecules appear to be the likely precursor to a combination of non-organic mineral and organic molecules developing, naturally, from non-living to organized, living matter.
These theories are helpful and very interesting for their contribution to our knowledge. However, what I find most interesting about them is the way in which they embody an extremely important religious question, a question about the fundamental meaning of "living" and life itself. These studies revolve around a belief, or an assumption, that matter is non-living in the first place, and that something occurs that converts or changes the non-living matter into living matter. This could be called "the miracle of life." In fact, a great deal of popular literature and religious thought makes reference either directly and explicitly, or often indirectly and implicitly to this concept of "the miracle of life." But, suppose Nature does not recognize a boundary between non-living and living matter. Suppose that all things are alive and nothing in the universe is "non-living." That would mean that there is one miracle only, the miracle of existence. And that would mean that life is not a "new thing," not something that begins by some event that occurs after the beginning of the existence of the universe. This viewpoint would mean that the matter in the universe is itself alive, all of it, and there is nothing that is non-living. This would mean that if we hold life sacred, then all things are sacred, even the stones and the black smoke of hot mineral water that boils up from the floor of the oceans, the stars, and all that occupies the space between the stars. The board and the nails in the carpenter's hands are not less sacred, not less alive, than the carpenter.
My theory of what distinguishes living from non-living is symbolized by the letter "G". This is not contrived, but a logical metaphor, because the letter G is a closed circle but with an "open door." And this is in fact the common characteristic of everything that we label as "alive." Everything that lives is like a single-celled organism: it possesses a boundary of some form, a skin or a shell or a protective membrane or layer, and this "skin" or membrane exercises a certain level of control over what "comes" inside the living cell boundary and what "goes" from inside the living cell to the outside of the boundary. This is why boundaries are important at all levels of living things and living colonies, communities and societies. We always hold boundaries as being very important. Without the boundary that controls the exchange of material, in both directions, the object would not be deemed to be alive. This is, in my opinion, the best physical and chemical and social definition of life. It is a kind of "unified" multi-disciplinary definition of life. It applies in many fields, from the field of micro-biology to the fields of geography and politics. It also applies in a very special way to religion and any theory of religion, because it competes with other fundamental issues as possibly being the most fundamental issue of religion.
4) What is the Most Fundamental Issue of Religion?:
We are accustomed to believing, and assuming without doubt, that the most fundamental issue of religion is whether or not there is a creator God, and stated perhaps more correctly in terms of sociological science, the question is not whether there is such a God but whether you or I believe in the existence of such a creator God. Now, that implies obviously that many people will argue that if you "believe in God," then you are religious, and if you do not believe in God, then you are not religious. This issue is instantaneously problematic, all social scientists know, because we have never devised a means to determine whether a person believes in God or does not believe. All we have to go on, customarily, is what people say. There are millions of Americans and others around the world who actually believe that if someone says "I believe in God," that their voice establishes that they do in fact believe in God and they are in fact "a religious person." However, historians and sociologists have been trying to tell us for centuries, if not forever, that people who have claimed to believe in God have committed the most horrible crimes against both individuals and the human enterprise. They have burned and tortured, slaughtered and devoured. They have destroyed buildings and tools and books of knowledge. They have used every tool of destruction to oppose those who disagree with their interpretation of what they usually call "the laws of God." Therefore, among sociologists and clergy, and among the general public throughout the world, there are also many millions who count the words "I believe in God" as worthless conformity and manipulative bullshit. The way that we determine what a person believes is by observing what they do.
If we can think, momentarily, that perhaps whether or not a person "believes in God" is not the most fundamental issue of religion, then you may be open to my proposal that what I am describing here, on these pages, is in fact the most fundamental issue of religion: Is the universe comprised of separate non-living and living matter, or is all matter alive? I propose that this is the most fundamental issue of religion, because it overwhelmingly affects any concept related to the "sanctity of life," and because it removes "the miracle of life" and replaces it with "the miracle of existence," and because it includes the concept that God is not the issue. Life is the issue. My reading of the New Testament Gospel tells me that what is identified as "the kingdom of heaven" and attributed to Jesus' voice, is in fact "the Kingdom of Life." And, this Kingdom of Life is not another world, not a real or "super-natural" realm that is separate from where we are. While we live here on this planet Earth, we are in the Kingdom of Heaven and in the Kingdom of Life. The feeling of separation is an illusion that occurs because of a misunderstanding of ancient religious teachings and of Jesus' teachings. In any case, nothing can separate people more deeply than this issue about what is alive. Regardless of whether you believe there is some form of God or not, what will separate people far more deeply is that some will believe everything is alive, and others will persistently impose a hierarchy on all things claiming not only that some things are not alive, but that among the living things there is a hierarchy, and some living things are more sacred than others, and some people are more sacred than others. This is what you have seen, is it not?
When Jesus asks his disciples who do they say he is, Peter responds, "You are the son of the living God." Jesus praises him for this answer, implying that there is some essential accuracy, some specific reality that Peter has identified by saying "the living God." (Matthew 16: 13-20; Matthew 22: 29-33) Possibly the most important issue conveyed here is lost to us because we live in the modern world. In ancient times, and for many people today whose religion is still a religion of ancient times, the Gods or gods with power over human life included the gods of the dead, meaning the gods or God of those who were not alive, the God of spirits and ghosts and monsters from Hell. The God that often concerned people the most was the feared God, Satan, the Powerful and Hidden and Evil One who could capture their souls, make them sin, take them forever into the Sainthood of Evil and make them into the ugly, disgusting and terrifying opposite of good, and of life. Death. Irreversible Loss. Therefore, when Peter said, "You are the son of the living God," Peter was clearly separating Jesus from any of the "evil ones" that people feared would have controlling and punitive power over them. Notice, my friends, that Jesus was clearly known to his disciples and is known to us today as a God of forgiveness and mercy, like Allah, "merciful and compassionate." He is therefore logically a son of the Living God and no relative of the sick and punitive Satan. I believe that Peter's statement and Jesus' teaching actually went deeper than this. Peter's understanding of Jesus' teaching was correct. Jesus taught that all things were alive, that all of existence was to be respected and revered. When the religious authorities presented themselves as proud of their genetic and religious heritage, their membership in the House of Israel, Jesus said to them that they should not be so proud of their ancestors, because God could raise up new ancestors from the stones. (Matthew 3: 7-12) As is the tragic reality, the mistaken clergy tell us this is some kind of metaphor for the power of a metaphorical God. For me, it is a scientific statement of physical reality that Jesus taught consistent with all of the legitimate physical science that Jesus taught. When Jesus said that "God" could raise up new ancestors, new people, from the stones, he was saying what is true about the real physical universe: the stones are alive and the transition or conversion from stone to human being is not as big a change as we think. In terms of the processes of Nature in the living universe, the distance between a stone and a human mind is short. This is not a reflection on the mind any more than it is a reflection on the stone. The thoughts of the living brain begin in the stone. Living things begin with the stone not because the stone "comes alive" through some miracle. It is already alive. The atoms are alive. This is the Kingdom of Heaven and the Kingdom of Life. I do not "mix" religion and science. I reconcile them and join them into the single truth. Nature does not recognize a spiritual reality that is distinct and separate from physical reality. Neither do I, because I understand the imperative that we understand Nature accurately, or perish.
5) The Molecular Mirror Method for Identifying an Anti-Virus:
We are at risk to be extinguished by disease. We have reason to believe that a virus or a new form of tuberculosis or blood infection could kill a billion people or more over the period of a year. Plants and animals do not exist in accordance with a "food chain" or a food ladder. Nature is more accurately described as a food cycle or a food circle. The larger eat the smaller, but the smallest consume the larger either while they are living or after they are deceased. After the lion eats the gazelle, the bacteria eat the lion. The bacteria and the viruses and all of the microbes consume everything that does not have an effective defense. Methods for fighting disease should not be patented, but should be placed in the public domain by law.
A Molecule and its Mirrors: from "fiat" to algorithm
Both bacteria and viruses, but especially viruses, employ their proportional shapes to invade and consume larger organisms. The essence of why they can do this is because molecules have polyhedral surface shapes. Although the electrical charge character of a molecule plays a role in how that molecule behaves, and how it can bond with specific atoms or other molecules, the primary source of atomic and molecular bonding is proportional polyhedral shapes (according to the LICEA theory) or mirror shapes, and the proportional shapes and electrical charges are both a direct result of the electromagnetic character of the nuclei of the atoms. When searching for an anti-virus, medical researchers, I believe, use our medical inventory of knowledge about viruses to help identify a virus and its "shape" or the mechanism by which it attaches to or penetrates particular tissue cells in the human body. The method could be described with the phrase well known in mathematics "by fiat." This phrase, "by fiat," means that the problem is resolved simply by "doing it," meaning by doing a tedious series of unique steps and solving the problem as though it is a unique problem that has to be solved without reference to any generic problem solving algorithm. An algorithm is different from solving a problem "by fiat," because with an algorithm you are treating the problem as though it can be solved with a generic or standard set of steps. An algorithm is exactly that, a set of standard steps to find the solution to a known type of problem.
My suspicion then, presented here as the final and most important part of the Message of the Ancients, is that the polyhedral atom allows for an algorithm to find an anti-virus or an anti-bacterial agent. I call the simplified and therefore fundamental principle of that algorithm the Molecular Mirror Method, because it is just that, an algorithm to find the mirror proportional shape of a molecule. The subject molecule would be the molecule that enables the viral or bacterial enemy to invade the larger organism. A mirror molecule, if it can be carried in the human bloodstream by any of our immune system cells, would function in most cases as an anti-viral or anti-bacterial agent, because it would enable the disease fighting cell to either capture or neutralize the invading virus or bacteria. The key concept here, of course, is that we could develop a geometric algorithm, driven by the ordinary mathematics of algebra and physical geometry, to identify the subject molecular shapes and then their mirror shapes. Instead of having an inventory of viruses in our human encyclopedia, we could develop an inventory of molecular shapes that are our disease invaders. This would be similar in some ways to the project of identifying the "human genome." However, we would probably not have to identify the "enemy molecules" in such large numbers as human genes. Although there must certainly be a very large number of molecules possible, only a limited number, perhaps in the thousands or tens of thousands, will be a threat to our organ tissues. As such an inventory grew, our ability to cope with new invader molecules would grow also. Our "system" for fighting disease would be similar to what we do now, but would take us a layer deeper, from using knowledge of the viral agent as a whole to using knowledge of the viral tool, the molecule that enables it to enter the home of the organism like a burglar with a crowbar. By disabling the tool, we disable the virus. This is what we do in a sense already, but with the Molecular Mirror Method, we can develop an algorithm, or algorithms, that could be computer programmed. This approach has the potential to enable us to find an anti-viral agent in hours instead of in months.
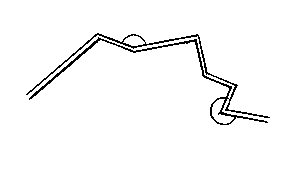
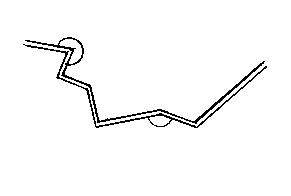
Here is a sample of the most simplified character, for identifying a molecular shape as having sides and angles, or vertices, and then using a computer program to identify the mirror shape.
The first drawing represents a section of an invader molecule comprised of side lengths and angles or vertices. By computing or calculating the mirror shape, we can then identify, from our inventory of molecular shapes, limited by the parameters of organic chemistry, molecules that could serve as tools to capture or neutralize that particular invader molecule. The mirror shape, reversed from left to right, is shown in the second drawing. We still would have to engineer the relationship between this molecular tool and the immune cells in the human body. In the real world, the shapes and the mathematics of the geometry would be far more complex, because they would apply to real, three-dimensional molecules, not just the two-dimensional plane shown here.
We are taught by the great teachers and by Nature to be good stewards. But good stewardship is far more important than humans have understood it to be. It is not optional. We do not own the planet we live on. It is owned by others smarter than we are. The Great Phi Pyramid is a mark of ownership. We will not be allowed to take ownership of the planet Earth unless we demonstrate that we are good stewards and we know why we are good stewards. We must demonstrate that we know the universe is geometrical and we know how to control our own population density. If we do not demonstrate both the ability and the commitment of good stewards, we will not be allowed to be in control of the planet Earth. Good stewardship is not something like generosity or gentleness. It is the highest level of evolution of an intelligent being. Intelligent beings, technological beings, who are not good stewards are not allowed to be in control of a planet.
6) The Programmable Mathematics of the Molecular Mirror Method:
Simplified Molecular Mirror Method
Angles written in degrees, dimensions left to right.
Number of steps for this polygon section are: 13
1) Side = 1.250000000000000
2) Angle = 119.000000000000000
3) Side = 0.500000000000000
4) Angle = 222.000000000000000
5) Side = 0.812500000000000
6) Angle = 90.000000000000000
7) Side = 0.500000000000000
8) Angle = 233.500000000000000
9) Side = 0.375000000000000
10) Angle = 88.000000000000000
11) Side = 0.375000000000000
12) Angle = 283.000000000000000
13) Side = 0.625000000000000
Begin outer mirror dimensions, right to left:
13) Mirror Side = 0.625000000000000
12) Mirror Angle = 77.000000000000000
11) Mirror Side = 0.375000000000000
10) Mirror Angle = 272.000000000000000
9) Mirror Side = 0.375000000000000
8) Mirror Angle = 126.500000000000000
7) Mirror Side = 0.500000000000000
6) Mirror Angle = 270.000000000000000
5) Mirror Side = 0.812500000000000
4) Mirror Angle = 138.000000000000000
3) Mirror Side = 0.500000000000000
2) Mirror Angle = 241.000000000000000
1) Mirror Side = 1.250000000000000
Begin outer mirror dimensions, left to right:
1) Mirror Side = 1.250000000000000
2) Mirror Angle = 241.000000000000000
3) Mirror Side = 0.500000000000000
4) Mirror Angle = 138.000000000000000
5) Mirror Side = 0.812500000000000
6) Mirror Angle = 270.000000000000000
7) Mirror Side = 0.500000000000000
8) Mirror Angle = 126.500000000000000
9) Mirror Side = 0.375000000000000
10) Mirror Angle = 272.000000000000000
11) Mirror Side = 0.375000000000000
12) Mirror Angle = 77.000000000000000
13) Mirror Side = 0.625000000000000
7) Experimental design to address the polyhedral atom issue:
Of course, theories must be tested by experiment. The theory that the atom is a polyhedron or a "living crystal" is not easily tested. We hardly know what really occurs at the atomic level. All of twentieth century physics is theory imperfectly supported by a variety of experiments where the conclusions are inferred, not proven concretely. We do not see the atoms and we do not see the many "particles" that we infer from lines on photographic plates or film. Much of what we infer is from evidence in the electromagnetic spectrum outside of the spectrum of ordinary visible light. All of atomic theory is based on technical results, instrumental measurements, not on certainty. Before despairing of the difficulty of testing this theory, note that there already is a great deal of scientific documentation that is consistent with the polyhedral form of the atom. The DNA and RNA molecules are described as "zipping" and "unzipping" because of a "matching" connection of some kind between a pair of molecules. Viruses are deemed to have the capacity to penetrate a cell wall because they possess a molecular shape that mimics a safe molecular shape, and in this way "enters by deception." The immune system appears to be able to "read" bacteria and identify them as needing to be captured and ejected, meaning excreted. The immune system appears to be able to "read" viruses also, and can, if given enough time, either mimic the virus or develop the means to disable the virus and bring its invasion and consumption of the organism to a halt. The data suggest that proportional shape is everything in the war between viruses and the defensive cells of the immune system. There is no proof that atoms are spherical.
In thinking about how the polyhedron theory could be tested, thus far, I have thought that the supposed spherical nature of the "orbital" model might be the key. Possibly we can either rule out or discredit, or at least question the orbital model by showing experimental results that are different from those the orbital model should provide. In the orbital or planetary model of the atom, the electron is believed to be revolving around the nucleus in a uniform circular motion. In this model the velocity of the electron is expected to be uniform. There is no observation or theoretical justification for the velocity of the electron to change. In the polyhedron model that I have presented here, the velocity does change. It changes dramatically. For an extremely short interval of time the electron stops its forward velocity and spins in place, then proceeds again in a straight line trajectory that forms an angle with its previous straight line trajectory, and forms the sides of a polygon or polyhedron. There may be a statistical experiment that could compare experimental results with what should occur according to statistical processes. Certain types of experiments involving "beaming" particles at atoms should also be reconsidered. It is my understanding that "new particles" fly away from an atom in various directions and they appear to have passed through the atom and changed their character in the process. This could be an incorrect interpretation of the instrumental data. It could be that the particles are bouncing off of the polyhedral surface of the atom, the flat, angled surface being comprised of a kind of force field. That could be the explanation of why the particles "change character" and travel in various different directions, because of the angle of the polyhedral surface that they collide with.
Shoot-the-electrons experiment:
If we have accepted information about the velocity of the electron and the size of its orbital trajectory, then we have a model for the motion of electrons over time. If we have data for the velocity and probable trajectories of particle "bullets" that can be "shot" at an identifiable cluster of atoms, we should be able to make a prediction, using statistics, of how many electrons will be "hit" and produce a detectable signal over averaged intervals of time. This statistical calculation would be based on the data for an "orbital" atom. If the atom is a polyhedron, the actual experimental results should be measurably less than (or perhaps more than) what would be expected to result from the orbital atom, because in the polyhedron atom the electrons are stopping and spinning momentarily before they proceed. If such a result is obtained, deviating from what would be expected statistically, it should be taken as evidence at least that the theory of the polyhedron atom should be explored further. Either I myself or others who work in the field of atomic research will conceive of ways to test the polyhedron atom theory.
8) The Story of Time Tweet
A long time ago I learned a lesson from a mentally retarded boy named "Time Tweet." He was given the name "Time Tweet" because he repeated that phrase periodically all day. He repeated that phrase because he was asking a question: "Time to eat?" meaning, of course, "Is it time to eat?" This was of great interest to him. He was not a trim fellow. He was by nature anxious as to when the time to eat was near. It seemed possible that his limited mind knew no other joy.
Time Tweet was one of many retarded children living at a residential educational institution. I was among a few staff hired to provide a recreation program during the summer months. Time Tweet would be labeled differently today, as "developmentally disabled" instead of "mentally retarded." However, whichever phrase is used, it means his cognitive ability, his knowledge and ability to perform mental work, was severely limited. An IQ test of Time Tweet would have resulted in a full scale score well below 70. He was a pleasant boy, likeable like a baby, but clearly did not have a bright future. Still, a friend of mine at the school struck up a conversation with me about the problem of Time Tweet, who was not able to look at a clock and read it. He could not "tell time." In fact, he seemed to not even have a clear awareness of what "phase" of the day it was: morning, afternoon, evening, night. My friend, who I knew only briefly and whose name I have forgotten, started talking about how we might be able to provide a special clock for Time Tweet and his limited peers. Instead of numbers from one to twelve, the clock would show four simpler divisions: breakfast, lunch, dinner, bedtime. This would provide Time Tweet with the information that was of greatest interest to him, and offer him an opportunity to develop a deeper awareness of what occurred, and what should occur, between breakfast and lunch, lunch and dinner, dinner and bedtime. For example, not eating, exercise, activity, not time to eat.
That concept, the concept of the simpler clock, penetrated deep into my brain. It captured my imagination. A simpler clock for simpler brains. What was so difficult about reading a clock? Later in life I would learn a great deal more about the human brain, and about how people learn, and what various intellectual limitations look like. For example, working as a social worker for many years, I have met many youth who initially present as intelligent and fairly articulate, able to carry on an interesting conversation, but who it turns out cannot multiply and divide numbers, cannot make change, or cannot read the printed word because they have a form of dyslexia, and who often are master artists at hiding that fact. I have known a charming teenage girl who had many social skills, but was in special education because of significant limitations in her academic skills. She could not read a clock. You would never know that if you met her, but it was true. Something was "missing" from her mental machinery, or some part of her brain had been malformed or damaged, and as a result she could not read a clock. Why was that? How does this make any sense? How can children and adults function rather well socially but be unable to do ordinary arithmetic, or be unable to read words, or be unable to read a clock? I have also learned about how people learn from my own study of human learning and human memory. There is a theory, which I believe to be correct, that knowledge is memory and only memory. I believe, as many others do, that the key to knowledge and mental work and what we call "creativity" is how our memories are organized in our individual brain. Memories and categories of knowledge are not organized the same in every brain. The human brain is an amazingly "elastic" or individual organ. That is why we have billions of humans and every one of them appears to us to be different, unique in some way. Some students of the human brain, neurobiologists and others, believe or suspect that there is something more involved in what we call the possession of knowledge, something greater than just organized memories. I hope we will learn more about this soon. It will be the greatest help to us to know in detail and with certainty how we learn. The more we know about how we learn, the more we will understand how we make mistakes in our observations of the real world. But, lets return to Time Tweet, and what I learned from him.
While thinking about Time Tweet and his problems, I thought about other children who were limited in their mental abilities. I asked a question that many people have asked throughout the course of human history. How does this happen? What is it that seems so subtle that deprives an otherwise normal human being of the ability to do arithmetic, or read, or perform what we call "complex tasks?" When we study developmental disabilities, we find patterns in a child's history, such as high fevers, tragic conditions of body chemistry while the mother is pregnant, accidental head injuries, complications at birth. However, we know primarily only the gross apparent causes. We do not know exactly what parts of the brain are damaged. But, I have a suspicion. A suspicion to share with you that came to me from Time Tweet.
We see the clock as simple. Time Tweet does not. It is overwhelmingly complicated to him. Let me describe another task that would be simple for you, but not for Time Tweet or any developmentally disabled child or adult. Let's call this game "Sort the cards."
You will have a set of cards. Each card will have a shape, a color and a number. The card set will basically be organized as follows:
Shapes: circle, square, triangle, rectangle.
Colors: red, blue, green, yellow, white, gray.
Numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Now you see if every possibility is represented, there are 4 shapes, 6 colors, and 10 numbers, and that means there would be 240 cards. In this game of "Sort the cards," we can give you a variety of different assignments to test your ability to think quickly, and accurately, and perform "simple work" quickly. We could have two sets of cards that are the same, and have you and another person perform the same sorting task, and whoever finishes first is the "winner." As a reward, you get to eat something that you like! Sound funny? Well, it should not be so funny. This game is not very different from the way our real economic system works.
So, here is your first sorting task:
Select all the red cards with numbers less than 8.
Select all the cards that have a 9 or a 10.
Select pairs of cards that are either green or blue and the pair of numbers add up to 7.
Now the important question here is how are you going to do this. Is it going to be easy? Can you watch your mind working so that you can complete this sorting task accurately and quickly?
I can. That is, I believe I know how your brain and anyone's brain would go about performing this task, which appears at first to be a complex task. You would do it in steps. Whether you would be consciously aware of the steps or not, there is no doubt in my mind that you would break the task down into simple steps. You would not try to do all the steps at once or conceive the entire task as a single whole. This is what I learned from Time Tweet. I thought of Time Tweet when I once read that an airliner has a billion parts, or a million. I don't remember, but clearly a billion or a million is a lot of parts, too many for one person to keep track of, or to know where they go and how they get attached to the other parts. Therefore, an airliner, or a computer, or an automobile, or a clock is made of many parts, and somehow we are able to build them. We are able to solve complex problems. But, we are not able to solve complex problems by conceiving in our brains the entire complex task at once. We can perform complex tasks only because our brains possess the ability to break a complex task apart into a set of simple comprehensible tasks. This is essential. And I believe that what is missing or damaged in the brain of every person who is developmentally disabled, or mentally retarded, is that part of the brain that provides us with that crucial ability to break complex tasks into simple parts or steps. Without that ability, I am convinced that what happens is that the brain becomes overwhelmed and paralyzed by its own inability to proceed. But, you see, this produced a conclusion in my brain that is different from the conclusions of others.
Through some unique history and thinking of my own, I believe that all human beings, including myself, are mentally retarded. And my conclusion about why Time Tweet and all retarded people cannot succeed at the "Sort the cards" game is not because they are unable to comprehend the complexity of the task, but rather because their brains are not able to comprehend the simplicity of the task. Their damaged brains cannot break any task apart into separate simple steps. We can. And that is the source of our amazing abilities. Without this skill of seeing the simple steps that lead to completion of an enormously complicated task, such as building an ocean liner or a rocket ship, or a nation, we would all be as helpless as Time Tweet. We would not be able to do any of the things that sustain human civilization.
And, the conclusion I have been led to, and which is relevant to what I have presented here with regard to the myth of Pi exactly and medicine and the atom is that I believe we have made our real physical world appear far more complicated than it is. I believe that our brains do that, make things appear profoundly complex when in fact they are not. That is our "normal" form of mental retardation. We are, at a different level from Time Tweet, unable to perceive the simplicity of the world, and in our own way we are captivated by what appears to us to be extreme complexity. That is why I believe we have obtuse physics and math, and the concept that an individual has to master calculus and possibly other aspects of higher mathematics in order to "understand the universe." I believe this is nonsense and is not consistent with the evidence. Nature does not need mathematics to do anything that it does. And since mathematics is not needed, it is not applied. Nature is economical and does not "invent" anything new to do what can already be done. It makes no sense that an "intelligent" species would evolve that is not capable of understanding how the world works. If the human brain that evolved on Earth cannot comprehend the Earth, then the theory of evolution is entirely false. The theory of evolution makes sense only if the brains that evolve posses the capacity to understand the environment that must be understood. If a brain is characterized by constantly developing incorrect conclusions about how the world works, that brain is not a "survival trait" that enhances the likelihood of propagation of the species. A brain that persists in making mistakes in interpreting reality is like feet that cause an animal to trip and fall down, like eyes that see objects where they do not exist, like ears that hear sounds without the ability to locate the source of the sounds. Simply and finally stated: in order to be useful, the human brain must interpret the world correctly. If it does not, it is not a survival trait, and we can only add to the many concepts that we have misunderstood the perplexing question of how the hell did we evolve brains that cannot understand the reality in which the brain must survive?
In conclusion therefore, what I learned from Time Tweet is that we are a mentally retarded species, but we do have a chance to survive indefinitely so long as we hurry up and learn how the universe is simple and not as complicated as we have made it. I suspect we make the world more complex than it is so that we can sort ourselves into a hierarchy and feed emotions as primitive as any to be found in a bird or a rat.
This is why I am able to argue for the outrageous concept that the universe is geometrical and not mathematical. The ancients were more advanced than we are and they did not recommend that children be taught mathematics. They recommended that children be taught geometry, music, gymnastics and history. And the Pythagorean Theorem. They recommended that children be taught an appreciation of "proportion" because the study of proportion leads to a correct understanding of the universe. Calculus just teaches you how to throw things or predict the price of the next crop. These are impressive skills, but they are only short-term survival skills. To have a shot at survival indefinitely, you have to understand how Nature throws things and how Nature grows the next wild crop without counting or measuring anything.
9) The Secret of Life in the Universe:
To conclude this report I urge you once more to study proportion and will offer my last concise statement of The Secret of Life in the Universe.
A good way to study proportion is to begin with the Universality of Phi, Part C of The Precision of the Ancients. To expand upon my arguments regarding "proportion is everything" thus far, I will present here the calculated output of InvXpN01, which means Inverse of X, squared, equals X times N plus 1. This program uses the quadratic equation and formula to get pairs of numbers that possess these interesting proportional qualities. Look at the PS (positive solution) and the NS (negative solution). The PS is first. The NS is the inverse of the PS. The NS possesses a quality that should cause you to wonder. NS is that number which, when squared, equals B times NS plus 1. The "B" here is the variable "B" as in AX^2 + BX - C. A = 1 and C = -1. That's it. As explained previously, in AnyNrt01 the selected variable N equals C in the quadratic equation, therefore C is the variable that gets us the result we are seeking there. However, with InvXpN01 the selected variable N equals B, and therefore B is the variable in the quadratic equation that gets us the result we are seeking here.
In Volume 2, The Myth of Exactly Pi, under "Mathematical Note," I described some "adjustments" to the way that we use the quadratic equation (A* X^2 + B*X + C = 0) and the quadratic formula (immediately below) to get the calculated output of AnyNrt01.
Formula: -B (+ or -) square root of (B^2 - [4*A*C] )
-----------------> all divided by 2 * A
The primary adjustment was that we considered the value under the radical (B^2 - [4*A*C] ) to be a positive value, so that we would not have the impossible inconvenience of trying to compute the square root of a negative number. Also, when that square root value was part of the negative solution, meaning when the numerator was [-B - square root of (B^2 - [4*A*C] ) ], the "minus" total would be treated as a positive value also. In AnyNrt01, the variable C in the quadratic equation was the variable that got us the results we sought. But here with InvNpX01, the variable B gets us the results we want, and we assign C the negative value -1. Otherwise, we apply the same convention in InvNpX01 with regard to the total value under the radical and the "negative solution." We make them positive.
InvXpN01.cpp Inverse of X = X + N (2/6/2006)
Corrections entered on 3/18/06: minus signs entered for variable B in NS negative solutions, and html errors corrected in this quadratic equation section.
Based on X^2 + B*X - 1 = 0. Yields solution to
(1/X) = X + B, as in (0.618033988... and 0.414213562...)
Or, X^2 = (B * X +1),
PS = X^2 + 1.00*X -1 = 0.618033988750
NS = X^2 - 1.00*X -1 = 1.618033988750
NS^2= 1.00 * 1.618033988750 +1 = 2.618033988750
PS = X^2 + 2.00*X -1 = 0.414213562373
NS = X^2 - 2.00*X -1 = 2.414213562373
NS^2= 2.00 * 2.414213562373 +1 = 5.828427124746
PS = X^2 + 3.00*X -1 = 0.302775637732
NS = X^2 - 3.00*X -1 = 3.302775637732
NS^2= 3.00 * 3.302775637732 +1 = 10.908326913196
PS = X^2 + 4.00*X -1 = 0.236067977500
NS = X^2 - 4.00*X -1 = 4.236067977500
NS^2= 4.00 * 4.236067977500 +1 = 17.944271909999
PS = X^2 + 5.00*X -1 = 0.192582403567
NS = X^2 - 5.00*X -1 = 5.192582403567
NS^2= 5.00 * 5.192582403567 +1 = 26.962912017836
PS = X^2 + 6.00*X -1 = 0.162277660168
NS = X^2 - 6.00*X -1 = 6.162277660168
NS^2= 6.00 * 6.162277660168 +1 = 37.973665961010
PS = X^2 + 7.00*X -1 = 0.140054944640
NS = X^2 - 7.00*X -1 = 7.140054944640
NS^2= 7.00 * 7.140054944640 +1 = 50.980384612482
PS = X^2 + 8.00*X -1 = 0.123105625618
NS = X^2 - 8.00*X -1 = 8.123105625618
NS^2= 8.00 * 8.123105625618 +1 = 65.984845004941
PS = X^2 + 9.00*X -1 = 0.109772228646
NS = X^2 - 9.00*X -1 = 9.109772228646
NS^2= 9.00 * 9.109772228646 +1 = 82.987950057818
PS = X^2 + 10.00*X -1 = 0.099019513593
NS = X^2 - 10.00*X -1 = 10.099019513593
NS^2= 10.00 * 10.099019513593 +1 = 101.990195135928
Change to fractions:
PS = X^2 + 1.000000000*X -1 = 0.618033988750
NS = X^2 - 1.000000000*X -1 = 1.618033988750
NS^2= 1.000000000 * 1.618033988750 +1 = 2.618033988750
PS = X^2 + 0.500000000*X -1 = 0.780776406404
NS = X^2 - 0.500000000*X -1 = 1.280776406404
NS^2= 0.500000000 * 1.280776406404 +1 = 1.640388203202
PS = X^2 + 0.333333333*X -1 = 0.847127088383
NS = X^2 - 0.333333333*X -1 = 1.180460421716
NS^2= 0.333333333 * 1.180460421716 +1 = 1.393486807239
PS = X^2 + 0.250000000*X -1 = 0.882782218537
NS = X^2 - 0.250000000*X -1 = 1.132782218537
NS^2= 0.250000000 * 1.132782218537 +1 = 1.283195554634
PS = X^2 + 0.200000000*X -1 = 0.904987562112
NS = X^2 - 0.200000000*X -1 = 1.104987562112
NS^2= 0.200000000 * 1.104987562112 +1 = 1.220997512422
PS = X^2 + 0.166666667*X -1 = 0.920132881566
NS = X^2 - 0.166666667*X -1 = 1.086799548233
NS^2= 0.166666667 * 1.086799548233 +1 = 1.181133258039
PS = X^2 + 0.142857143*X -1 = 0.931119203401
NS = X^2 - 0.142857143*X -1 = 1.073976346258
NS^2= 0.142857143 * 1.073976346258 +1 = 1.153425192323
PS = X^2 + 0.125000000*X -1 = 0.939451221368
NS = X^2 - 0.125000000*X -1 = 1.064451221368
NS^2= 0.125000000 * 1.064451221368 +1 = 1.133056402671
PS = X^2 + 0.111111111*X -1 = 0.945986465407
NS = X^2 - 0.111111111*X -1 = 1.057097576518
NS^2= 0.111111111 * 1.057097576518 +1 = 1.117455286280
PS = X^2 + 0.100000000*X -1 = 0.951249219725
NS = X^2 - 0.100000000*X -1 = 1.051249219725
NS^2= 0.100000000 * 1.051249219725 +1 = 1.105124921973
Note the narrative explanation of the output of InvXpN01:
Where N = 2 = B, then 1* X^2 + 2 * X -1 = 0, the positive solution is:
-2 + square root of (4 - [4* 1* -1 ] ) = -2 + sqrt(8) = 0.828427124746...
------------> all (each) divided by 2
and the negative solution is:
-2 - square root of (4 - [4* 1* -1 ] ) = + 2 + sqrt(8) = 4.828427124746...
------------> all (each) divided by 2
PS = X^2 + 2.00*X -1 = 0.414213562373
NS = X^2 - 2.00*X -1 = 2.414213562373
NS^2= 2.00 * 2.414213562373 +1 = 5.828427124746
And where N = 3 = B, then 1* X^2 + 3 * X -1 = 0, the positive solution is
-3 + square root of (9 - [4* 1* -1 ] ) = -3 + sqrt(13) = 0.605551275463...
------------> all (each) divided by 2
and the negative solution is:
-3 - square root of (9 - [4* 1* -1 ] ) = + 3 + sqrt(13) = 6.605551275463...
------------> all (each) divided by 2
PS = X^2 + 3.00*X -1 = 0.302775637732
NS = X^2 - 3.00*X -1 = 3.302775637732
NS^2= 3.00 * 3.302775637732 +1 = 10.908326913196
Using a scientific calculator, you can check and see that we obtain the same results when B has a fractional value.
10) The Minus Line Issue: I have changed the quadratic equation to reflect reality:
The conventional application of the quadratic equation, where there can be no minus values under the radical, and one solution, the "negative" solution is discarded, does not reflect reality. The reason these traditional conventions do not reflect reality is because there are no minus values in the real physical universe. There are minus numbers in mathematics, and that is acceptable, but in order to reflect the reality of line lengths, there can be no line length that is assigned a negative or minus value. In mathematics there can be a line assigned a negative or minus value because of its position. But this is a human invention, not physical reality. In the real physical universe, there is no such thing as a minus line. All lines have length, which means positive length. Let's look at how constructed line lengths would work in conjunction with the quadratic equation.
Let's look again at the application of InvXpN01 where N = B = 3:
A = 1, B = 3, C = -1 as line lengths. The -1 line length simply means a line length of 1 but we are going to subtract it. Since we see that 3.302775637732... is the "negative solution" that we sought, we can look at how the implementation or execution of the solution works as an operation with straightedge and compass to construct the subject values as line lengths.
PS = X^2 + 3.00*X -1 = 0.302775637732
NS = X^2 - 3.00*X -1 = 3.302775637732
NS^2= 3.00 * 3.302775637732 +1 = 10.908326913196
If we can begin with our line length of 3.302775637732..., we construct the ratio of that line length over 1, by constructing a right triangle with the height being 3.302775637732... and the base being 1. Then we reconstruct a similar right triangle, with the same tangent, but with the base having a length of 3.302775637732... . In our reconstructed similar right triangle, the line length of the height A has to be 3.302775637732... squared, because it is equal to side B times the tangent. This is based on our "Main Algorithm" as described in Volume 1, The Precision of the Ancients. And 3.302775637732... squared equals 10.908326913196... which is now the line length of side A. We subtract the line length of 1 (C= -1) using our compass, and we then have a line length of 9.908326913196... . We then use the procedure for dividing a line into 3 equal lines and each of those three lines has a length of 3.302775637732... . The procedure for dividing a line into X equal lines is to first construct the line to be divided as a horizontal line. Then construct an acute angle at the left end point and above the horizontal line. Then construct the same acute angle below the horizontal line at the opposite (right) end point. On each of the constructed sides (above and below the horizontal line to be divided), mark off X equal distances with the compass. Then, using the straightedge, construct a straight line from the furthest marked point on the upper line to the right end point of the horizontal line to be divided. Then use the straightedge to construct straight, parallel lines from the upper points to the lower points. The horizontal line will then be divided into X equal line lengths. As is always the case, the precision of the construction depends on the precision of the instruments and the care of the operator.
However, we need to see how we can begin with a line length of 3.302775637732... . Let's look again at our quadratic formula equation:
Where N = 3 = B, then 1* X^2 + 3 * X -1 = 0, the positive solution is
-3 + square root of (9 - [4* 1* -1 ] ) = -3 + sqrt(13) = 0.605551275463...
------------> all (each) divided by 2
and the negative solution is:
-3 - square root of (9 - [4* 1* -1 ] ) = + 3 + sqrt(13) = 6.605551275463...
------------> all (each) divided by 2
Simply, the value under the radical is a line length of 9 plus a line length of 4, equals a line length of 13. We apply the procedure for construction of the square root of a line, which is described in detail in sqrtra02, under Part C) The Universality of Phi, in Volume 1, The Precision of the Ancients. We then have a line length of the square root of 13, = 3.605551275463... . Then with our compass and straightedge we add a line length of 3, to get 6.605551275463... . Then we divide that line in half to get 3.302775637732..., the line we now know we can construct to begin with.
This is a Proof of the Reality of Proportional Dimensions:
What I claim to have proven here, immediately above, is that what is true for this one instance is true for everything that you see on these pages that pertains to proportion and to the Universality of Phi, and what that means precisely is that all of the numerical proportional values can be constructed as line lengths and or ratios, and therefore they can be constructed as the dimensions of a real object. What is also proven here is that the "minus line lengths" are nothing more than the act of subtracting a line length from another. And, even if we have a calculation in the quadratic equation, or any equation, where the operation called for is to subtract a line length of 5 from a line length of 3, the actual and appropriate result is simply a line length of 2 and not a line length of minus 2.
The essential point of what is presented here regarding the "minus line issue," is that the "adjustments" I make to the application of the quadratic equation is actually a proposed reform of the doctrines of mathematics. I propose that the traditional application of the quadratic equation, where a "negative solution" is discarded does not reflect the real world. I propose that the traditional use of the quadratic equation, which is to find solutions to "second degree variables" is an error. The original and best application of the quadratic equation is to find proportional values which are in the real physical universe proportional dimensions. We can identify these proportional dimensions by using the quadratic equation with conversion of minus values to plus values as appropriate to reflect physical reality. The essence of proportion and of the quadratic equation is reflected in A*X^2 + B*X + C = 0 and more importantly, in A*X^2 = B*X + C because this equation, A*X^2 = B*X + C, is the equation at the core of "Chaos Theory" and the science of Proportion. This is the mechanism of proportion through which Nature does all that it does without counting or measuring anything. With this reformation in the use of the quadratic equation, we can re-discover Proportion.
In order to insert a little comic relief, let me discuss the "minus cow" problem, which is a kind of introduction to my mathematical proof, which is my work in process where I focus intensively on my argument that our mathematics is a cultural artifact and that Nature does not use anything more than proportion and addition to do all that it does. The relevant point to all of this work is to show that the universe is proportional and not mathematical.
11) The Minus Cow Problem:
In elementary school we learn that when a farmer has a hundred cows and he (or she) sells fifty of those cows (a "word" problem) we can label the 100 cows as +100 cows and the cows sold as minus cows, that is -50 cows. For all the years of schooling that follow the concept of "minus" and negative values is reinforced again and again. It is reinforced constantly in mathematics and in accounting and in business and in physics and every field of science. Plus is plus and minus is minus. There is a number line or "scale" and in the middle is a Zero (0) and to the right is the plus values and to the left is the minus values. If anyone had any problem with the minus cows in the young students' classroom, they were assured that in order to succeed in arithmetic, and mathematics and in human society, they had to recognize the existence of the minus cows. But, the truth is, any student who did protest was in fact correct. The minus fifty (-50) applies to the number, not to the cows. None of the individual cows was, or is, a minus cow. There are no minus cows in the real physical universe, no minus pigs, no minus dollars, no minus anything. Everything is just simply there, or here, or wherever it is. We can label it as "minus" when we subtract it or "take it away." However, again the ultimate reality is consistent with the perception of the child rather than with the sophisticated but abstract mathematical thought of the adult. When we "take away" something, we have to put it somewhere, and when we put it somewhere, we are adding it, making it a plus cow or plus dollar, or plus whatever it is. In physics, we have conservation laws. Whatever occurs, mass is conserved, and if you believe that energy and mass are interchangeable, or are "converted" one to the other and back and forth, there is a conservation of the total "value" of mass and energy no matter what event or process occurs. Matter is never destroyed and never vanishes from the universe. It can be converted into energy, but not annihilated. This brings us back to the cows, and counting, and accounting. In the field of accounting there is the double entry system, or double entry bookkeeping system. Basically, this is a business version of the conservation laws. Nothing is only subtracted, or only "minus." If money, or a number value, is removed (subtracted) from an account to pay for something, it must be added someplace else. If there is a debit, there is a credit somewhere to match the debit. This system dramatically reduces errors in accounting. It reflects reality. There are no minuses that are not matched by a plus. Getting back to our farmer, we have to acknowledge that the farmer is not alone in the universe, and if they sell (minus) 50 cows, some other farmer has bought (plus) 50 cows. The cows are just cows, and they are either always just cows or plus cows. With Nature, in the real physical universe, there are no minus farmers who get minus milk from minus cows.
The Discrediting of Religion or of Mathematics:
In the history of what we call western civilization, a process took place that we could call the discrediting of organized religion. That is, there was a time when the religious organization, or "The Church" held the highest authority, and that authority was beyond question. The Church was what I like to call "the exempt institution." By "the exempt institution" I mean that the Church could not be questioned by anyone who was not an official member, and it could not be questioned publicly by anyone who was an official member. No one other than a Church Scholar was permitted to legitimately question or discuss a "Church Doctrine." Later, over time, the authority of The Church was challenged. This was accomplished primarily, again over time, by the development of the fields of individual psychology and social psychology, the fields of study through which we examine human behavior. The Church wanted to continue to be "the exempt institution," and it rejected social science and "liberalism" because these patterns of thought removed the exemption and subjected The Church to examination or analysis. The behavior of the church, or churches, and of religious individuals, and all individuals and social groups was subject to "study" and examined, analyzed and picked apart. The patterns of religion and religious behavior were described as arising from complex and self-serving psychological motivations, such as fear, a desire to conform, a desire or need for ritual, and otherwise a set of social and emotional needs that are met by the various aspects of what we call "religion." This examination of churches and religion as a field of study did have the effect of removing "the exemption" and took away from the institutions of religion their previously absolute authority. The Church, therefore was not destroyed but was to a certain extent "discredited." It was discredited in the sense that it was no longer beyond question. Clergy and church organizations were and are now described as including the entire range of human flaws and social problems. They have factions, authoritarians, criminals, liars and thieves in "The Church." It is a human institution with human frailties. The "discrediting" of The Church certainly continues into our times with the gradual exposure of a significant percentage of Roman Catholic priests who are found to have used their position in society to have access to boys for sexual exploitation. This is a kind of glaring piece of evidence that although The Church still has authority, it is not exempt from examination.
The institution of mathematics is "the exempt institution" in western civilization today. It is beyond question. Mathematics is viewed as the ultimate reality, the description of reality that would not be questioned by anyone other than a lunatic. People in positions of power in government and business defend their plans and their positions by saying "We did the numbers." The unquestioned and unquestionable assumption in western society, and perhaps in most of the world today, is that if you can describe a plan or a concept or a "solution" in mathematical terms, you are in possession of a truth that is unassailable. You are scientific, and you cannot be challenged because mathematics cannot be challenged.
If you look for books about "creativity" in mathematics or science, you will find only babbling nonsense that simply repeats over and over again the assumption that any success in mathematics or science is inherently "creative." Such books do not examine either the meaning of creativity or the meaning of mathematics or science. They simply support the exemption of the institution of mathematics. Look, and you will not find a book or article anywhere, except right here on these pages, that truly questions and challenges the exemption of the institution of mathematics from examination. There are no works on "the psychology of mathematics" or "the sociology of mathematics." Why is this so? Because our society does not believe that mathematics can be examined using the tools of psychology and or sociology. Our society believes and teaches that mathematics is nothing other than the ultimate unquestioned truth, and that it is absurd to think that a mathematician or the behavior of mathematicians can be in some way "examined" and attributed to emotional or psychological motives. To human society today, mathematics is pure reason. But, I would argue that there is no human behavior that is pure reason. It cannot be. If a human is doing it, there is an emotion involved. In order for mathematics to lose its exemption, and to be truly examined, all doors would have to be opened and all bars removed. The assumption that mathematics is pure reason or is the ultimate reality would have to be suspended and mathematical behavior would have to be examined with the same intensive questioning as sexual behavior or family dynamics. The mathematics itself and the mathematicians would have to be exposed and subject to the same instruments of analysis as delinquent children and criminal adults. Why do they do what they do? Why do they believe what they believe? What do they believe, really? What are their myths and doctrines? What is the psychological function of mathematical symbols and mathematical language? Is the language deliberately obscure, deliberately coded so that only a few can read and write the language? What is the role of mathematics and mathematicians in society? How are mathematicians selected? What are their personality traits? How are they organized? Is there a hierarchy? How does it work? How are old authorities challenged by young authorities? How do mathematicians view "non-mathematicians?" How do we, all of us, use mathematics? Why do we periodically hear concerns that we Americans are "falling behind" in mathematics, when it looks like Americans are woefully ignorant of history? Why don't we hear concerns that Americans have no understanding of history? And ultimately, the question which I am addressing and intend to continue to address here and in a book in progress: Is mathematics an objective reality in the physical universe outside of the human mind, or is mathematics a cultural product of the human mind the same as the fine arts, music and ethnic language? My answer is that mathematics is a cultural product, a product of the human mind that exists only in the human mind, an artifact of abstraction that is nothing more than the persistent elaboration of counting and measuring. I say that Nature does not need mathematics and does not use or apply mathematics anywhere. The statement that "mathematics is everywhere" means to me only that we see mathematics everywhere because wherever we look we count and measure. The mathematics that is everywhere is projected from us, not discovered in Nature, but put there by our counting and measuring and calculating brains. I am convinced that the ancient saying that: "Man is the measure of all things," is a tragic error in translation. The correct observation is that "Humankind is the measurer of all things."
12) The Reformation of Mathematics and Science:
Mathematics needs to be discredited in order to be reformed. It needs to be exposed and no longer exempt from genuine and unbridled examination. In order to learn about the body, you have to dissect it. The Church was dissected. The Sacred Institution of Mathematics must now be dissected. We must do this because if we do not we are at risk to make a suicidal error in our conception of reality. There is evidence, I am arguing here, that the universe is proportional and not mathematical. There is evidence that everything that occurs does so only by means of proportion and that Nature has no need of mathematics to accomplish all that it does. This proposition must be seriously considered, or we will continue to re-produce a society that worships a false god. Mathematics is technology, the primary technology. Before we can engage our productive and creative impulses in accomplishing anything we must first count and measure. This is what we do. But we are being anthropomorphic, as usual, if we insist that because we do our technology that way, Nature's technology must be the same as ours.
A Need for the Reformation of Science:
The scientists are killing us. World War I and World War II, the military industrial complex, toxic chemicals everywhere. The exemption must be lifted. We are acting as though mathematics and science cannot be challenged, cannot be examined. The institution of science must be reformed. They are not choosing heretics to be burned. They are burning everyone and everything: birds, frogs, the oceans, the atmosphere, our foods. Why do people hesitate? Because mathematics and science are sacred. Mathematicians are the priests of "The Church" of America. How can we question the God of Science, the Ultimate Truth? They do not invite genuine examination. They do not accept genuine examination. They are exempt, and they will hold on to that exemption until the people insist that it is removed. The ethics of scientists and accountants, the mathematicians, are nil. Lying has become the primary tool of human commerce and industry. Scientists and accountants, the mathematicians, are hired to deliver the lies. You must attack and dissect them in order to save the human species from blind self-destruction. Think, people. We invented the wheel for travel. Nature did not select the wheel for any living organism. Nature is different. Nature is not a product of human design.
13) The Meaning is That the Pharaoh Points to the Secret of Life:
Now ask yourself what does all this mean. Does it mean anything special? What does the output of the program AnyNrt01 mean? Does it work for any N value? What does all of the material presented about "The Universality of Phi" and proportion mean? What does the output of InvXpN01 mean? All of the numerical results of AnyNrt01 and InvXpN01 are line lengths that can be constructed with a compass and straightedge, and the lesson intended to be conveyed here, the lesson that is the essence of the Secret of Life in the Universe, is that:
If we can construct these ratios and proportions, then Nature must be able to do so also.
What this means is that Proportion is Everything. What this means is that The Secret of Life in the Universe is Nature, the real physical universe, needs nothing more than proportion, the shapes and sizes of things, to organize and replicate itself. Proportion is sufficient, and therefore Nature did not invent anything further that was not necessary. Remember, Nature is economical, and apparently far more economical than we thought. Once again, this conclusion repeats and reinforces what was said and hinted at previously in these three volumes of The Rediscovery of Proportion: The Secret of Life in the Universe: There is only one miracle, the miracle of existence, not two. A second miracle, the "miracle of life" will not be found because there is no division in the universe between the non-living and the living. What is, is alive, everything. That is the Secret of Life in the Universe that was intended to be conveyed to us by the Great Phi Pyramid. Nature repeats its proportional patterns over and over again on a different scale. I, John Manimas, am not the first or the only person to argue that science leads one to the conclusion that everything in the universe is alive. A wonderful writer and thinker, Guy Murchie, presented this possibility in The Seven Mysteries of Life, Houghton Mifflin, Boston, 1978. He also wrote Music of the Spheres in which he discussed a similar and wide range of philosophical issues pertinent to the meaning of life, as compared to the idea of "not life."
This theory, original thought and report presented to you by John Manimas, is an act in the reconciliation of religion and science. It represents both a fundamental principle of science and a fundamental principle of religion. It serves as an explanation as to why the oldest religion on Earth is animism, the belief that everything is endowed with a spirit, and no spirit is disconnected, separate and alone. This theory is not to be taken lightly. It could be correct. If you think of yourself as a scientist, do not ever forget that: In order to survive we must understand the universe as it really is. Nature has no regrets, only survivors.
14) The Message From the Ancients:
This section presents a summary of Volumes 1-3 of The Rediscovery of Proportion: The Secret of Life in the Universe
The Message From the Ancients was not sent by one means only.
The Message sent by philosophy:
It is sent to us by ancient philosophy, in the statement that Proportion is Everything. This statement is an iconic means to communicate the same concept as Nature repeats the same patterns on a different scale, the basic principle of modern "Chaos Theory." The statement that proportion is everything is also an accurate statement of the fundamental truth of the Natural Universe. Nature, the universe, is proportional, not mathematical. No computations are necessary. In fact, in order to do what it does, nature needs only proportion and addition, and probably unrecorded counting. That is, in order to accomplish what it does, Nature probably needs to count, but the counting does not need to be named or recorded, just counted and compared and then discarded as a variable that has achieved its purpose and is no longer needed. The ancients knew this, at least four thousand years before us.
The Message sent by the Great Phi Pyramid:
The Great Pyramid is a Phi pyramid. It has the value of Phi and the square root of Phi incorporated in its proportions. The Great Pyramid therefore presents in a monumental icon the essence of the reality that proportion is everything. It also conveys, together with the hypotenuse-laid-down geometrical procedure, and the pentangle, and the Eye of Ra, an emphasis on the relationships of proportional values, the use of the quadratic equation to reveal proportional values, and the fact that the ancients knew the value of Pi as accurately as we do, at least four thousand years before us. Proven here, in Volume 1, The Precision of the Ancients, is the fact that they knew how to construct the value 3.14155655389944902222112102645257... as a line length, shorter than infinite Pi, 3.1415926535897932384626433832795..., by only thirty six millionths of a unit, and the closest value to infinite Pi that is constructible with only the compass and straightedge.
The Message sent by the Pentangle:
The pentangle repeats proportional values of Phi, emphasizing the importance of proportion.
The Message sent by the Hypotenuse Laid Down and the Eye of Ra:
The hypotenuse-laid-down geometrical procedure, and the pentangle, and the Eye of Ra, reveal the geometric construction steps that yield the closest value to infinite Pi that can be constructed with only the compass and straightedge, known to the ancients, at least four thousand years before us.
The Message sent by all of the above:
The study of proportion leads to an understanding that infinite Pi, the value of Pi intensively studied and virtually worshipped by mathematicians, does not exist as an actual physical dimension of any object in the universe. Infinite Pi is an infinite mathematical series, and only an infinite mathematical series, and that means it could not be the dimension of a real object unless that real object had an infinite number of sides, which is impossible. Therefore, the Message From the Ancients conveys to us the vital truth about the real physical universe that objects that appear to us to be circular and globular are in fact polygonal and polyhedral.
Since any real solid object must be polyhedral in shape, the atom is therefore polyhedral, a crystal. This student and investigator, John Manimas Medeiros, has concluded that the atom is a living crystal that generates its unique polyhedral shape by the regular firing of the nucleus sending outward for a very short distance an electromagnetic pulse, or "vibration," that stops and spins the electrons for an extremely short period of time. That is this investigator's atomic theory, but whether this theory is correct or not, the Message From the Ancients does convey to us that the universe is comprised of polyhedral shapes, not circular and spherical objects with dimensions that are equal to infinite Pi.
The Message sent by Time Capsules:
The "tombs" in the Valley of the Kings are not tombs. They are time capsules. The argument that the intelligent ancients were superstitious primitives who put priceless treasures and their own servants, members of their household, in burial vaults so that they could take all of these things -- furniture, sculpture, wall paintings, tools, servants, jewelry, tapestries and clothing, even their pets and their chariots -- with them on their journey to a separate spiritual world is criminal deception. They are obviously time capsules created to convey to the children of the future, meaning you and me, the fact that the ancients were an advanced civilization. A primitive or ordinary ancient culture could not have produced what is in those time capsules. The mummies also convey to us what is probably the most important message of all, the final clue to why the Message From the Ancients was sent in the first place. The mummies reveal that the ancient kings and queens suffered from disease. Why would they want us to know that? Because the ultimate purpose of the message is to tell us a vital truth that we need to know. That vital truth is that disease is the greatest threat to the survival of an intelligent species. A human civilization can survive all of the natural disasters, flood, volcanoes, earthquakes, fire, hurricanes, tornadoes, tsunamis, and all of these combined, including meteors and sudden climate change. However, the one natural disaster that can extinguish an intelligent species is disease. Disease can be the final phase of evolution on a life supporting planet. After the intelligent species multiplies to enormous numbers, in the billions, a virus evolves that consumes them all in a cosmic instant. And the cycle begins again. Unless... that intelligent species understands exactly how the universe works, and can produce an effective defense against every possible disease.
Who will hear and act upon these ideas?
That the universe is proportional and not mathematical will be an astounding and disturbing proposition for many people, especially mathematicians and physicists, but we must not allow mathematical doctrines to obstruct human progress. Question authority. Examine religion. Examine mathematics and physics, the exempt institutions and entrenched authoritarian religion of western civilization.
The Pyramid Mark:
The Great Phi Pyramid is a mark on the planet Earth to signify to travelers that Earth is owned and managed by the Shepherd Kings. The Shepherd Kings are a group of intelligent species who nurture and liberate good stewards to take care of life in at least one corner of the universe. Earth is an incubator planet where an intelligent species is nurtured and tested periodically for disease resistance. Our value in the development of good stewards is our potential for disease resistance. We live on a warm, water planet where a very large number of diseases, of various types, can thrive. Therefore, we must have high quality disease resistance in order to live on Earth. The two main challenges accepted by the Shepherd Kings are: 1) the evolution of intelligence toward the highest level, which is the achievement of good stewardship; and 2) the evolution of disease resistance. Disease resistance is necessary for living on the surface of a planet, but far less necessary for living in what we call "space," the Kingdom of Heaven. The Pyramid Mark tells us we are owned and being supervised and protected, for a purpose, and that purpose is to become good stewards with effective disease resistance, good stewards who can live indefinitely and join in the work of nurturing and liberating life in the universe. We have been taught that we can live "forever," but that is a word that we should not use in this context. Jesus taught us: "Heaven and Earth shall pass away, but my words shall not pass away." That means that because Jesus' words are the truth, they are the most enduring thing in the universe. In the real universe, the truth is the only thing that endures forever. Everything else is temporary. For all practical purposes, in comparison with forever, living indefinitely means far less than forever, though still a very long time. Long enough to enjoy the trip.
On the other hand, an intelligent species that developed technological skills, but for some reason could not evolve to be a good steward, would most likely be considered armed and extremely dangerous. If we on Earth do become good stewards, then the Kingdom of Heaven will tell us, just as the Good Master does in Jesus' parable of the Fairthful Servant (Matthew 25) "...because you have been faithful over a few things, I will set thee over many."
- End of Three Volume Series -
Permissions and Translations, Limited permissions granted by the author:
By posting my work here, on these web pages, I have exercised my copyrights as an author, but have surrendered none. I can, however, allow further reproduction and sharing of my work on restricted terms if I chose to do so. I have chosen to grant to everyone who becomes aware of this work on the Internet, to reproduce one paper copy and one electronic file copy for themselves, and one to be given to another person, without charge or any fee for the cost of the copy. I gave it freely, you must do the same. Remember the principle of copyright law: Anyone who benefits financially from the work of the author is obligated to compensate the author. The facts of geometry and mathematics can be neither patented nor copyrighted, but crediting an individual who made a scientific discovery is a common courtesy practiced throughout the world.
Citation suggested: Manimas, John. The Rediscovery of Proportion, "Welcome to Aquarius," Medicine and the Polyhedral Atom, www.jmanimas.com, Volume 3 (March 6, 2006).
Rules for translations
The author does not have the financial resources to commission and approve translations from English to other languages; however, it is not the author's intention that this important information be available only in the English language. Therefore, please observe the following rules for any unofficial and unapproved translations of this entire work or any part of it:
A) Any translation into another language will please carry the following copyright notice and unofficial translation notice in BOTH ENGLISH AND THE OTHER LANGUAGE:
"Copyright 2006. John Manimas Medeiros. All rights reserved.
This is an unofficial translation from the original American English, at www . jmanimas . com , to [name of language], that was not examined or approved by the author, John Manimas.
The translators ( [names of translators] ) accept full responsibility for any errors in this translation or any misleading interpretations of the original work in English."
B) Neither the translator nor anyone else may accept any payment of any kind for copies of the translated work. I have given it to the world for free. You must do the same.
C) The author would appreciate receiving notice of any unofficial translations. Such notices can be sent by postal mail to: John Manimas, P.O. Box 536, Bellows Falls, VT 05101
D) The author would be pleased if unofficial translations are soon made available in Spanish, French, Russian, Chinese, Portuguese, Japanese, Arabic, Swahili and Italian.
Link to: (Welcome) or (Geometry Alpha Index) .