Hiram Key Simplified

The Hiram Key Simplified

This amazingly simple construction is proposed to reveal both the natural value of one in proportion and a proposed theory that this proportional reality enables matter to measure itself before it assembles itself.

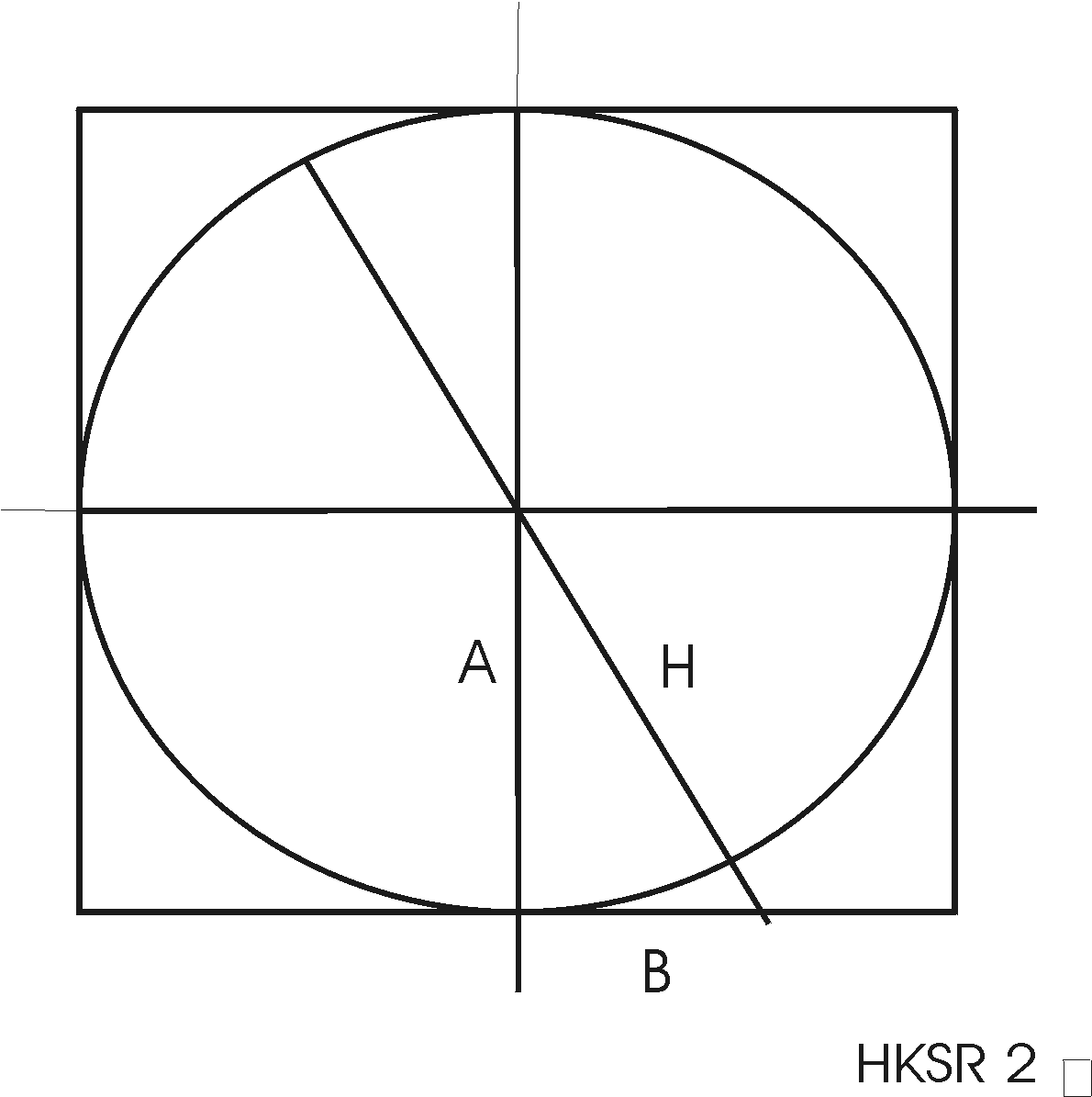
Using only the compass and straightedge, construct a circle and the external tangent square, which means the sides of the square are tangent to the circumference of the circle. Use a convenient size. Observe that we can construct numerous angles (G) greater than 45 degrees extending from the lower right horizontal side of the square passing through the center of the circle, and then extend such a line, being the hypotenuse of a right triangle, upward further to a point intersecting with the square at the upper left horizontal side of the square. That line X now is a diameter of the circle plus the smaller, additional length that extends outside of the circumference of the circle to the vertex of the angle of interest (G) that is greater than 45 degrees. It is important to observe that by nature (or Pythagorean formulas) the shorter hypotenuse that extends outside of the circumference has a line length value that is exactly equal to the reciprocal value of X, the same as being equal to the inverse of X.

Observe the cosine of the angle, and the inverse, the secant. Then we contemplate, but do not measure or designate, that the value of the base of the right triangle has a line length value of 1. In our right triangle with sides A (altitude), H (hypotenuse) and B (base), we now have H = secant of angle G, B = 1, and A = sqrt(H^2 -1). These are familiar facts. However, consistent with accepted geometric theorems and corollaries, there is another set of fixed proportional relationships. Let (1/X) = R.

A = X^2 -1 and H = X^2 + 1 X = A + A + R

2X 2X

AND, most important of all, no matter by what factor we multiply the three sides of the right triangle, the proportion of Side B to all other lines in the construction is 1, one and only one by nature, and not by arbitrary operator designation. Drawing below:

And, if and when we can begin with the right triangle where H = sqrt(5), and the value for line length X = sqrt(5) + 2, and then proceed to construct a straight line length equal to pi exactly, we can then construct circles and squares exactly equal in area, and therein we are enabled to discover and understand how the real, physical universe measures and assembles itself. It is reasonable to think of these geometric facts as the secret of life in the universe, the acronym being SOLITU. This is what the Pythagoreans were pointing to when they told us to construct a pentagon and that "proportion is everything." Construction of pi exactly as a straight line is described in the Unification Construction, included on the jmanimas website as "SOLITU- G"